Alteryxの予測カテゴリに配置されている「線形回帰」の結果レポートについて詳細に解説していきます。Alteryxの回帰モデル(1)で解説した内容とカブる部分もあるかもしれませんが、ご了承下さい。
線形回帰ツールの結果を詳細に読み解く
それではレポートを詳細に読み解いて行きたいと思います。1ページずつ読み解いていきましょう。リッジ回帰、ラッソ回帰の場合は異なったレポートになります。
項目としては以下の通りとなります。
- 基本の要約
- 残差
- 係数
- 残差標準誤差
- R-二乗
- F統計量
- タイプII ANOVA分析
- 基本診断プロット
- 95%信頼区間があるパフォーマンス診断プロット
- モデル適合メトリック(モデルあたりの平均)
1ページ目
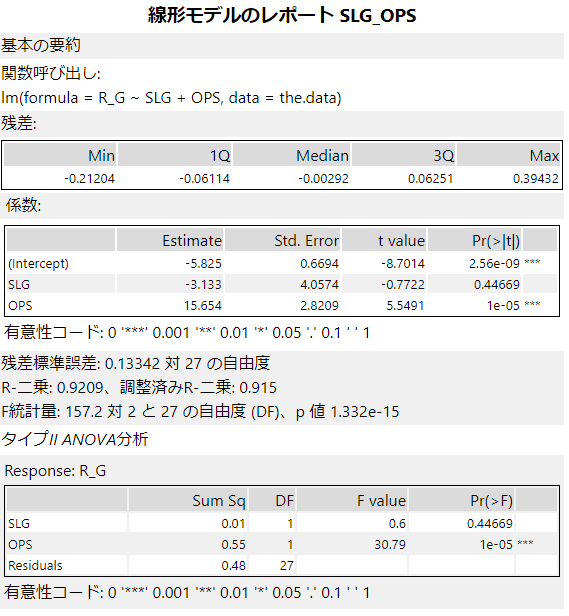
基本の要約
関数呼び出しは、ツール内部でRツールが呼び出しているコード部分になります。lmというのが線形回帰の関数です。より詳しく知りたい場合は、Rの関数のマニュアルなどをあたるということも可能です。
残差(Residuals)
残差とは、定義としては「回帰直線から垂直に伸ばした各データまでの距離」となります。つまり、予測値と実際の値との差分です。
ここで表示されているのは、残差がどのような分布をしているかの統計量です。最小値、最大値、第一四分位数、第三四分位数、中央値で構成されています。
係数(Coefficients)
Estimate(推定値):回帰モデル y=ax+bの「a」にあたる。いわゆる傾き。
Intercept(切片):回帰モデル y=ax+bの「b」にあたる。切片。
この2つを使うと、回帰式は以下のような関数であることがわかります。
SLG*-3.133+OPS*15.654-5.825Std.Error(標準誤差):回帰係数の推定値の標準誤差
t value(t値):t検定の検定量。各予測変数が0かどうかの検定結果(0であれば不要ということになるので、この値が十分大きければ0ではない、と言えるということになります)。
Pr(>|t|)(p値):t vlaueを元にしたp値。0.05未満であれば、統計的に有意(ターゲット変数と相関がある)。
p値の右の項目の有意性コードについては、p値が「*」は0.05未満、「**」で0.01未満、「***」で0.001未満となります。基本的に「*」が多いほうが重要な予測変数となります。
残差標準誤差(Residual standard error)
日本語的に少し訳がおかしいのですが、「Residual standard error:0.13342 on 26 degrees of freedom」というのが元の文章です。つまり、自由度は26で、残差標準誤差は0.13342ということになります。
残差標準誤差は残差のばらつきです。自由度は、レコード数(30)-選択した予測変数(2)-1で計算されています。
R-二乗、調整済みR-二乗
回帰モデルの適合度を図るパラメータです。
R-二乗(Multiple R-squared):決定係数。0-1の間の値を取る。0.5以上であれば精度が高いとされる。単回帰分析の回帰モデルの適合度を示します。
調整済みR-二乗(Adjusted R-squared):決定係数。0-1の間の値を取る。0.5以上であれば精度が高いとされる。予測変数が多いとR-二乗値は増加するので、それを調整したものを重回帰分析の場合は使います。重回帰分析の回帰モデルの適合度を示します。
つまり、予測変数が1つしかない場合はR-二乗を見て、複数ある場合は、調整済みR-二乗を見ます。
F統計量(F-statistic)、自由度(Degrees of Freedom)、p値(p-value)
F統計量は、モデルの適合度を評価するための指標ですが、値が大きい方が良いです。F統計量をもとにp値が計算されているので、基本的にはp値を見ておき、p値が十分に小さいかどうかを見れば良いと思います。
ここでのF検定は、回帰式そのもの(複数の回帰係数)が、ターゲット変数に対して効果があるのかどうか、を検定するものです。
ちなみに、レポートの日本語訳が少し変です。「F統計量:157.2対2と27の自由度(DF)」と書かれていますが、英語だと「F-statistic 157.2 on 2 and 27 DF」となります。ここでは、F統計量は157.2となり、2とあるのは回帰モデル内で選択した予測変数の個数です。次の27は、レコード数(30)-選択した予測変数(2)-1で計算された自由度です。最初の自由度を第一自由度、2つ目の自由度を第二自由度と言います。
p値(p-value):F統計量を元にしたp値。有意性コードにあったように、0.05以下であれば統計的に有意ということになります。
タイプII ANOVA分析
ANOVAとは、ANalysis Of VArianceの頭文字を取ったもので、分散分析です。係数の項目にあるような形で、どの予測変数がモデルに重要か、誤差の分散の確認やモデルの適合度を判断することができます。
項目はそれぞれ以下のとおりです。
平方和(Sum Sq):各予測変数の二乗和。
自由度(DF):自由度は予測変数に対して1が割り当てられます。一番下にあるResidualsの行にある自由度は、レコード数(サンプル数:ここでは30)-各予測変数に割り当てられた自由度-1で計算されます。
F値(F value):F統計量です(前述のとおり)。
p値(Pr(>F)):F統計量を元にしたp値。
p値の右にある「*」は前述の有意性コードです。
2ページ目
2ページ目は、モデルの基本診断プロットとなります。この4つのグラフを確認することで、線形回帰の信頼性を確認することが可能です(ここは、Alteryxの回帰モデル(1)に記載した内容と同じです)。
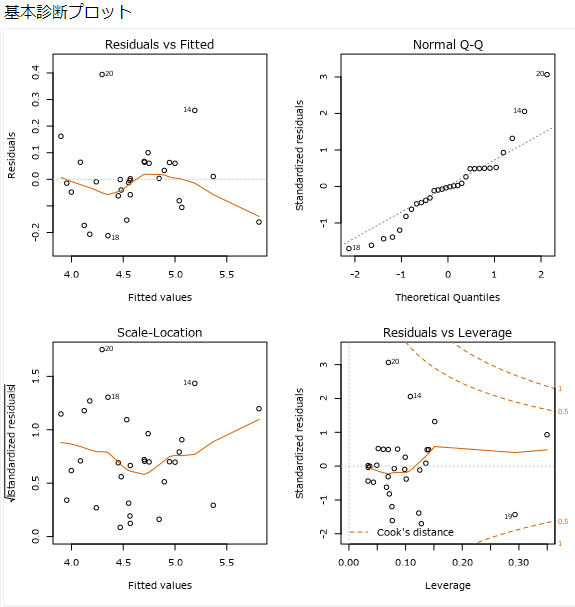
Residuals vs Fitted(残差-推定値)
横軸は予測値、縦軸は、予測値と実際の値との差(残差)。三点について確認できます。線形性:残差が0付近にあること。分散の均一性:残差が0の先の周りに水平な帯状にあること。外れ値の有無:残差の分布を見て、明らかに外れているものがあるか?
Normal Q-Q(残差のQ-Qプロット)
Quantile-Quantileプロットを略してQ-Qプロットと呼びます。残差が正規分布に従っていれば、直線状にプロットされます。重回帰分析では残差は正規分布に従っているという前提があり、これが崩れているようであれば、モデルの見直しが必要です。
Scale-Location(残差の正の平方根-推定値)
Scale-Location(残差の正の平方根-推定値):横軸は予測値、縦軸は残差の正の平方根。残差のばらつきを確認することができ、点が均等に広がった水平線が理想的です。
Residuals vs Leverage(標準化残差-てこ比)
横軸は、ターゲット変数のレバレッジ(てこ比)、縦軸は標準化残差。レバレッジが大きく、標準化残差が大きいものがあるとモデルの予測に影響を与えているものがある、ということになります。これらのデータに対して何かしら処理を行うことでモデルの適合度が高くなります。つまり、グラフにある破線をクックの距離(Cook’s Distance)といい、クックの距離の外側にあるようなデータは回帰結果に影響を与えています。これらのデータを除外することで、回帰結果への影響を変えることができます。
3ページ目
3ページ目は、2ページ目の続きです。
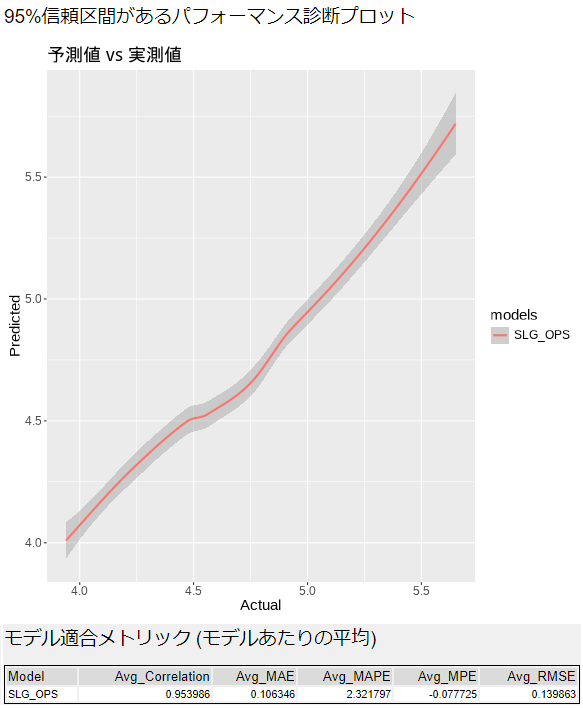
95%信頼区間があるパフォーマンス診断プロット
実際の値を横軸、予測値を縦軸にしたグラフです。直線状になっていると、まんべんなくパフォーマンスが出ていると言えるでしょう。特定の領域で差分が大きいようであれば、非線形になっている可能性もあります。
モデル適合メトリック(モデルあたりの平均)
相関係数(Correlation)、MAE、MAPE、MPE、RMSEの平均が出力されており、回帰分析のモデル評価指標が出力されています。
いずれも、それぞれ計算方法は異なりますが、予測値と実際の値にどれくらいの差があるか、という内容を出力しています。
相関係数(Average_Correlation)は1もしくは-1に近いと強い相関を持つ、ということになります。逆に、正負関係なく0に近い場合、相関が弱いということになります。
その他(MAE、MAPE、MPE、RMSE)は予測値と実際の値の差分なので、小さいものが優れています。MAE、MAPE、MPE、RMSについては、似たような言葉ではありますが、基本的にすべてError(誤差)なので、予測値と実際の値の差分となります。
MSE(Mean Square Error)平均二乗誤差
線形回帰の場合は、この平均二乗誤差が最も小さくなるように回帰直線が引かれます。計算方法は、実測値と予測値の差分を二乗したものの平均となります。
MAPE(Mean Absolute Percentage Error)平均絶対パーセント誤差
実測値と予測値の差分を実測値で割った値の絶対値の平均を取ります。割合で出したものとなります。割合なので基準もあるようで、一般的に10%未満で高い予測精度、10%~20%で良好な予測精度、20%~50%で妥当な予測精度、50%以上で低い予測精度、とのことです。
MAE(Mean Absolute Error)平均絶対値誤差
単に、実測値-予測値の平均を取ったものです。
RMSE(Root Mean Squared Error)二乗平均平方根誤差
実測値-予測値の二乗の平均を算出し、最後に平方根を取ったものです。
誤差を平均的に評価するのがMAE。RMSEは先に誤差を二乗しているため大きな外れ値や誤差がある場合悪い値になるので、外れ値や誤差を中心に評価できます。
気をつけるポイントとしては、予測値と実際の値がどれだけ差分がないか、という内容ではありますが、過学習(オーバーフィッティング)はここでは判断できないため、他のデータを使って精度が出るかどうかの検証も必要です(そのため、通常はホールドアウト法などを使って別のデータでの検証を行うのが普通です)。
参考URL
回帰分析の1ページ目の用語について説明が記載されています。
回帰分析の評価指標である、決定係数、RMSE/MAE/AICなどについて書かれています。
Rの関数の出力についての解説がされています。
Rの出力の分散分析表、F分析について解説されています。
F検定についての解説。
t検定について詳しく書かれています。
Anova Type2の平方和について記載されています。


コメント