Alteryxの予測カテゴリに配置されているモデルについて解説していきます。
今回は回帰専用の3つのモデルを解説します。
- 線形回帰(Linear Regression)
- ガンマ回帰(Gamma Regression)
- ポアソン回帰(Count Regression)
この3つのモデルは、ターゲット変数の分布で使い分けることができます。すなわち、線形回帰は、直線上に分布すること。ガンマ回帰はガンマ分布、ポアソン回帰はポアソン分布になっていることです。これは、分布分析ツールを使うことで、どのタイプに分布しているか、ということを確認することができます。また、Alteryxの線形回帰ツールは設定によりリッジ回帰、ラッソ回帰を使い分けることが可能です。
なお、非線形のデータについては、スプラインモデル、ニューラルネットワークなどを使用することになります。
線形回帰(Linear Regression)

線形回帰は、「線形関係に基づいて変数間の関係を評価するためのモデル」を作成します。線形関係ですので、データをプロットしてみるとに直線で表現される必要があります。
例えば、Alteryxの線形回帰ツールのサンプルワークフローの入力データのうち、R_GとOPSという項目を散布図にしてみます。
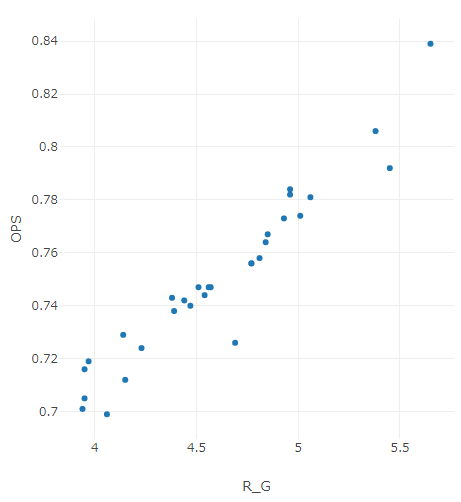
左下から右上に一直線上に並んでいるように見えませんか? 線形回帰は、予測変数とターゲット変数が一次方程式(y=ax+b)の形で表現されるような関係であるものをモデル化します。具体的な計算としては、最小二乗法という方法で直線を求めるようになっています。基本的にはこのデータの散らばりは正規分布になっているのが前提です(これをパラメトリックな手法といいます)。
また、重回帰分析(予測変数が複数ある場合)は、予測変数の標準化などを行いスケールを合わせることで、各予測変数の重みを正確に知ることができますし、外れ値の影響なども軽減することができるため、重回帰分析の場合は予測変数の標準化を行うことも検討すべきです。
設定
基本の設定は、モデル名を入力し、以下のようにターゲット変数と予測変数を選択するだけです。
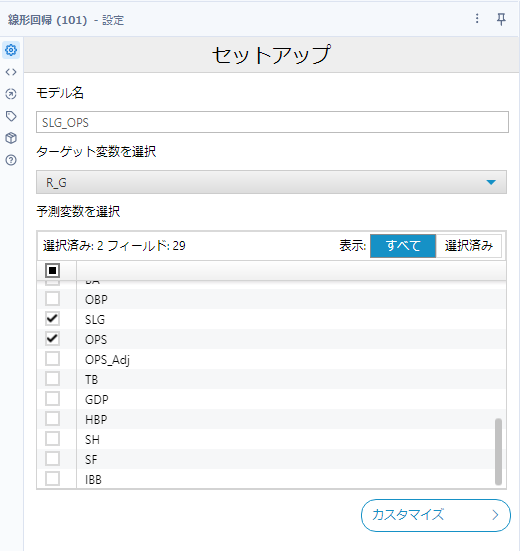
ただし、線形回帰ツールには多彩なオプションが用意されています。右下にある「カスタマイズ」ボタンをクリックすると、詳細なカスタマイズが可能です。ちなみに、デフォルトはオフです。
ちなみに、メインのオプションは、「モデル定数を省略する」「重み付き最小二乗に重み変数を使用する」「正則化回帰を使用する」の3つしかないのですが、正則化回帰のオプションが色々あるので、以下のスクリーンショットではかなり多彩なオプションがあるように見えるかもしれません。
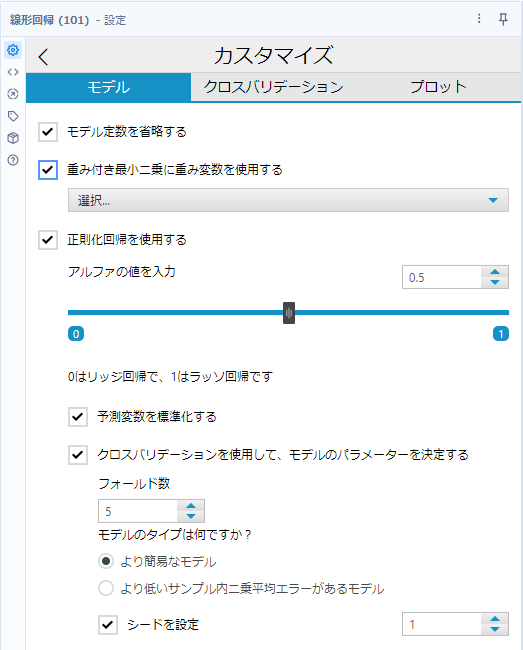
一通り表示を行いたかったので、上のものはデフォルト値ではないことに注意してください。
モデル定数を省略する
回帰式の定数項を強制的に0にします。例えば、予測変数が0になるときにターゲット変数も0になるような場合にはチェックを入れて強制的に0にします。
重み付き最小二乗に重み変数を使用する
最小二乗法で計算する際に重みをつける変数を指定します。
正則化回帰を使用する
このオプションは、リッジ回帰、ラッソ回帰を利用可能にできるオプションです。バーを右端にするとラッソ回帰(つまりアルファの値が1)、左端にするとリッジ回帰(アルファの値が0)となります。真ん中のアルファが0.5ではElasticNetになります。いずれも線形回帰の過学習を抑制するためのオプションです(その代わり、訓練データに対しての当てはまりは悪くなります)。なお、ラッソ回帰は「不要な変数の効果が0になりやすくなる」、リッジ回帰は「訓練データに対する過学習が抑えられる」、ElasticNetは両者の中間でバランスを保つ、という性質をもっています。
なお、正則化回帰オプションを使用すると、F検定ツールは利用できません。
また、このオプションをオンにすると、レポートの形が大きく変わります。
予測変数を標準化する
チェックを入れることで予測変数を標準化します。リッジ回帰、ラッソ回帰の場合は標準化は必須のため、元々のデータが標準化されていない場合はこのオプションを有効にしましょう。
クロスバリデーションを使用してモデル パラメータを決定する
フォールド値
クロスバリデーションでデータを分割する際の折り返しの数です。値が大きいとモデルの品質はあがりますが、小さい方が高速に動作します。
モデルのタイプは何ですか?
相関を取るときのモデルのタイプを決めます。
- より簡易なモデル(Simple Model)
- より低いサンプル内二乗平均エラーがあるモデル(Model with lower in sample standard error)
シードを設定
クロスバリデーションの再現性を確保するためのシード値です。
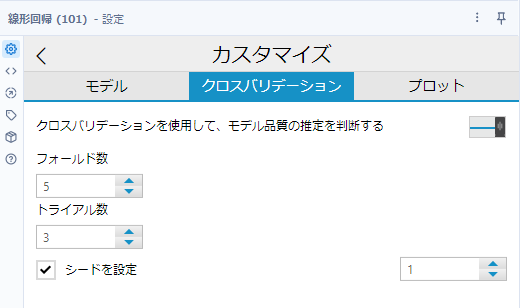
「クロスバリデーション」タブは、正則化回帰以外の際に使えるクロスバリデーションの機能です。
クロスバリデーションを使用して、モデル品質の推定を判断する
クロスバリデーションは日本語では「交差検証法」といいます。データをいくつかに分割し、トレーニングデータ、テストデータを入れ替えながら学習を行うことで、過学習を防ぎます。
フォールド値
クロスバリデーションでデータを分割する際の折り返しの数です。値が大きいとモデルの品質はあがりますが、小さい方が高速に動作します。
トライアル数
クロスバリデーションを繰り返す回数を設定します。フォールドは各トライアルごとに異なる方法で選択され、全体的な結果はすべての試行の平均となります。トライアル数も多いほどモデルの品質はあがりますが、小さい方が高速に動作します。
シードを設定
クロスバリデーションの再現性を確保するためのシード値です。
結果を読み解く
それではレポートを読み解いて行きたいと思いますが、概要レベルに絞って解説します(詳細は別のページで行います)。なお、リッジ回帰、ラッソ回帰の場合は異なったレポートになります。
1ページ目
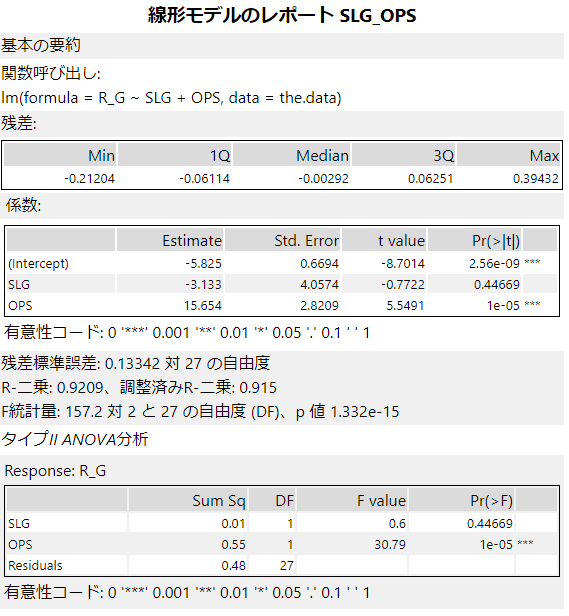
係数(Coefficients)
ここで見るべきは、p値(Pr(>|t|))とその右隣の星(*)の数(有意性コード)です。
この「*」の数は、簡単に言えば予測値に対してどれくらい影響を与えているか、ということになります。「*」が一つでもあれば、統計的に影響を与えているということになります。
「*」の数については、上のp値の値によって決まります。「*」はp値が0.05未満、「**」で0.01未満、「***」で0.001未満となります。
つまり、どの予測変数が重要か、ということがここでわかります。
R-二乗、調整済みR-二乗
予測変数が1つのみであれば、R-二乗を見ます。予測変数が2つ以上あれば調整済みR-二乗を見ます。値は0~1の間の値を取り、判断基準としては1に近づくほどモデルの適合度が高い、ということになります。一般的には0.5以上であれば精度が高い、とされます。
F統計量(F-statistic)、自由度(Degrees of Freedom)、p値(p-value)
F統計量は、モデルの適合度を評価するために指標ですが、値が大きい方が良いです。F統計量をもとにp値が計算されているので、基本的にはp値を見ておき、p値が十分に小さいかどうかを見れば良いと思います。
この例であれば、十分小さな値(0.05以下)となっているため統計的に有意と考えて差し支え有りません。
2ページ目
2ページ目は、モデルの基本診断プロットとなります。この4つのグラフを確認することで、線形回帰の信頼性を確認することが可能です。1ページ目よりよりモデルの詳細を確認することができます。
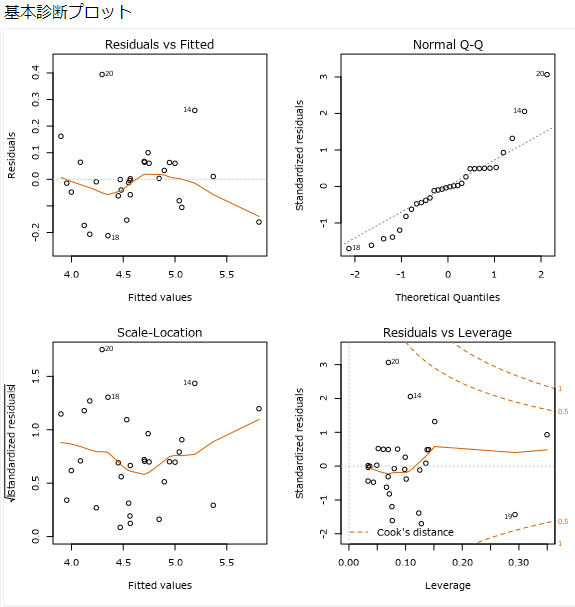
Residuals vs Fitted(残差-推定値)
横軸は予測値、縦軸は、予測値と実際の値との差(残差)。三点について確認できます。線形性:残差が0付近にあること。分散の均一性:残差が0の先の周りに水平な帯状にあること。外れ値の有無:残差の分布を見て、明らかに外れているものがあるか、というところが確認ポイントです。
Normal Q-Q(残差のQ-Qプロット)
Quantile-Quantileプロットを略してQ-Qプロットと呼びます。残差が正規分布に従っていれば、直線状にプロットされます。重回帰分析では残差は正規分布に従っているという前提があり、これが崩れているようであれば、モデルの見直しが必要です。
Scale-Location(残差の正の平方根-推定値)
Scale-Location(残差の正の平方根-推定値):横軸は予測値、縦軸は残差の正の平方根。残差のばらつきを確認することができ、点が均等に広がった水平線が理想的です。
Residuals vs Leverage(標準化残差-てこ比)
横軸は、ターゲット変数のレバレッジ(てこ比)、縦軸は標準化残差。レバレッジが大きく、標準化残差が大きいものがあるとモデルの予測に影響を与えているものがある、ということになります。これらのデータに対して何かしら処理を行うことでモデルの適合度が高くなります。つまり、グラフにある破線をクックの距離(Cook’s Distance)といい、クックの距離の外側にあるようなデータは回帰結果に影響を与えています。これらのデータを除外することで、回帰結果への影響を変えることができます。
3ページ目
3ページ目は、2ページ目の続きです。
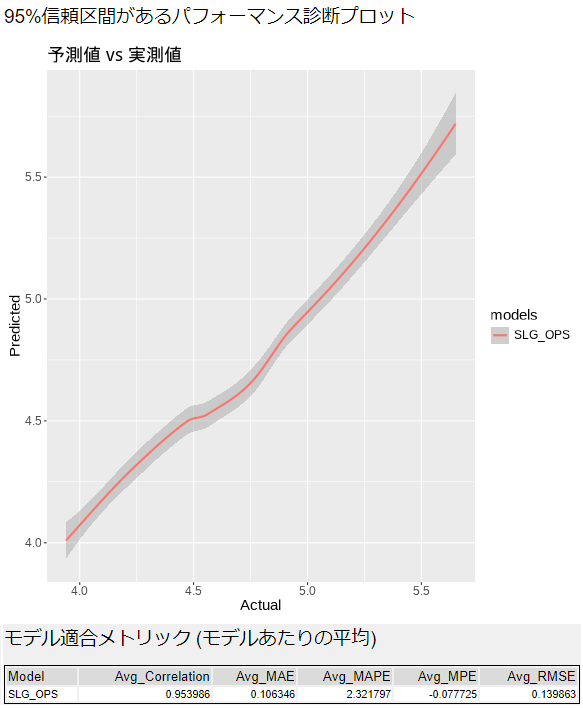
95%信頼区間があるパフォーマンス診断プロット
実際の値を横軸、予測値を縦軸にしたグラフです。直線状になっていると、まんべんなくパフォーマンスが出ていると言えるでしょう。特定の領域で差分が大きいようであれば、非線形になっている可能性もあります。
モデル適合メトリック(モデルあたりの平均)
相関係数(Correlation)、MAE、MAPE、MPE、RMSEの平均が出力されており、回帰分析のモデル評価指標が出力されています。
いずれも、それぞれ計算方法は異なりますが、予測値と実際の値にどれくらいの差があるか、という内容を出力しています。
Avg_Correlationは予測値と実際の値の相関となっており、絶対値が1に近いほど精度が高い、ということになります。
それ以外の指標(MAE、MAPE、MPE、RMSE)は予測値と実際の値の差分なので、小さいものが優れています。MAE、MAPE、MPE、RMSについては、似たような言葉ではありますが、基本的にすべてError(誤差)なので、予測値と実際の値の差分となります。
誤差を平均的に評価するのがMAE。RMSEは先に誤差を二乗しているため大きな外れ値や誤差がある場合悪い値になるので、外れ値や誤差を中心に評価できます。
気をつけるポイントとしては、予測値と実際の値がどれだけ差分がないか、という内容ではありますが、過学習(オーバーフィッティング)はここでは判断できないため、他のデータを使って精度が出るかどうかの検証も必要です(そのため、通常はホールドアウト法などを使って別のデータでの検証を行うのが普通です)。
ガンマ回帰(Gamma Regression)

ガンマ回帰ツールは、「ガンマ分布で厳密に正のターゲットを1つ以上の予測変数と関連付けます」。つまり、基本的にターゲット変数はガンマ分布である前提となります。ガンマ分布は正の整数である必要があります。
つまり、以下のように分布しているデータを予測するために使われます(パラメータで形状は変わります)。
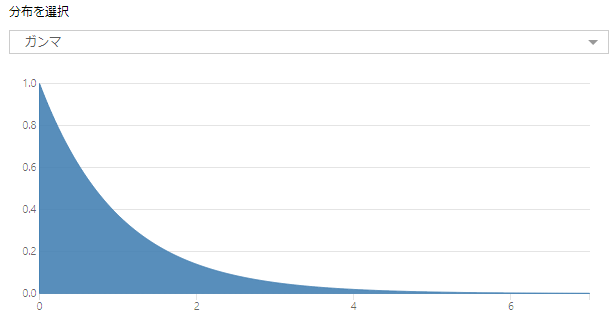
Wikipediaによると、「信頼性工学における電子部品の寿命分布」「通信工学におけるトラフィックの待ち時間分布」「所得分布」などが該当するようです。
設定
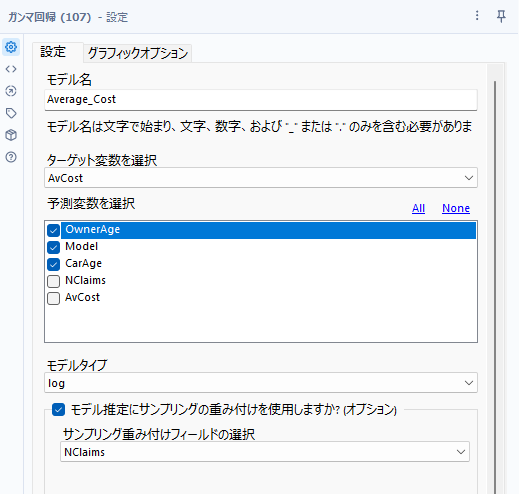
設定は上の通りです。基本はターゲット変数と予測変数を設定していくことですが、モデルタイプが選択可能です。
モデルタイプ(線形予測子と結びつけるためのリンク関数)は以下3種類から選択します。
- log(対数関数)
- inverse(逆関数)
- identity(恒等関数)
一般的にはデフォルト値のlogがよく使われます。
また重み付けフィールドを指定することも可能です(「モデル推定にサンプリングの重み付けを使用しますか?」)
結果を読み解く
ガンマ回帰のレポートは以下のとおりです。使っているRの関数は「glm」となり線形回帰と異なります。
1ページ目
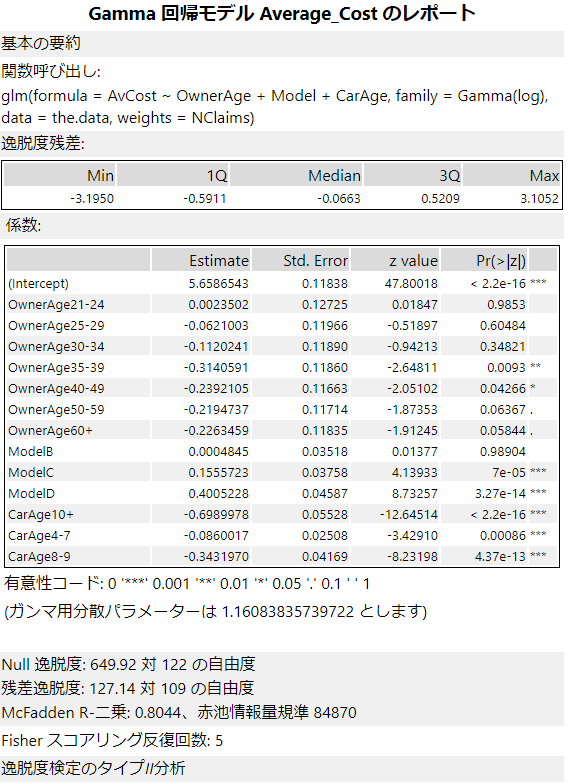
線形回帰と異なるポイントがいくつかあります。
係数
係数については、線形回帰ツールと同じ見方をします。t valueの代わりにz valueが使われていますが、p値に応じて有意性コードが与えられ「*」の数が決まるところは同じプロセスです。線形回帰ツール同様、「*」が多くついている予測変数が重要です。
残差逸脱度(Residual deviance)
残差逸脱度は値が小さいほど適合度が良いということになります。
McFaddem R-二乗(McFadden R-Squared)、赤池情報量基準(Akaike Information Criterion)
McFaddem R-二乗(McFadden R-Squared)は、線形回帰の決定係数に相当するもので、見方はR二乗値と同様に見てください。すなわち、値の範囲は0~1の間を取り、1に近いほどモデルの適合度が高い、ということになります。
赤池情報量基準(Akaike Information Criterion)は略してAICなどと呼ばれることが多いです。モデルの選択基準で、値が小さいのが良いモデルです。
2ページ目
最初の表は「逸脱度検定のタイプII分析」のグラフとなっています(タイトルだけ1ページ目にあります)。
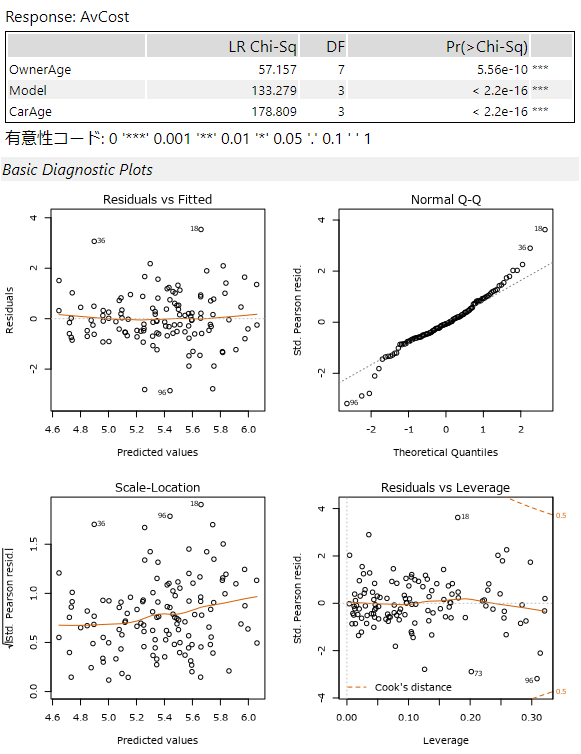
ちなみに、ガンマ回帰のレポートにはRMSEなどのレポートはでてきません。
ポアソン回帰(Count Regression)

ポアソン回帰ツールは、非負の整数値(0、1、2、3など)をターゲットとして1つ以上の予測変数と関連付ける回帰モデルを作成するツールです。
つまり、以下のように分布しているデータを予測するために使われています。
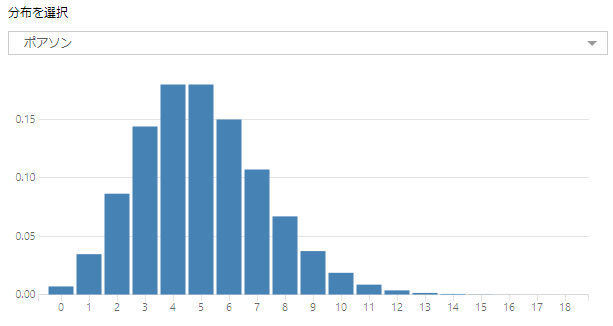
具体的な例としては、「ある人が所定の月に特定のレストランに来店した回数」、「あるいは特定の携帯電話アカウントに関連付けられた電話番号の数」とのことです(Alteryx Helpより)。離散的である「回数」というものを扱う場合の回帰モデルです。
設定
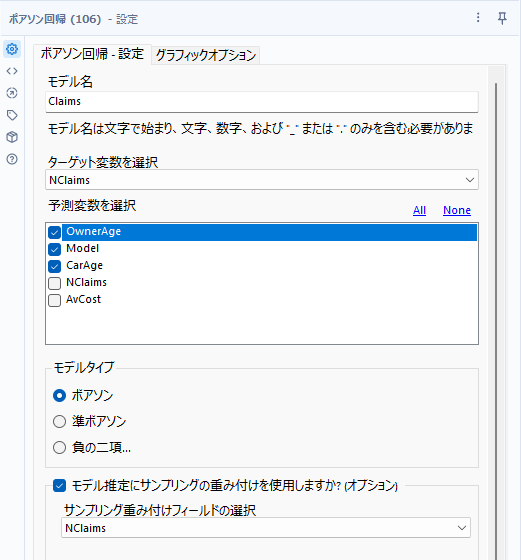
設定としては、モデル回帰と重み付けフィールドの選択が可能です。オプションはほぼガンマ回帰と同様です(同じRの関数を使っているからかと思います)。
モデルタイプは以下3つから選択可能です。
- ポアソン
- 準ポアソン
- 負の二項
負の二項を選択した場合は「シータの値」を指定することができます。デフォルトでは「auto」です。
選択の基準としては、ポアソンの場合は、ターゲット変数の平均値と分散値が等しいという前提となっています。負の二項は、ターゲット変数の平均値と分散に差があっても問題ありません(ポアソン分布より分散が大きい場合に使う)。
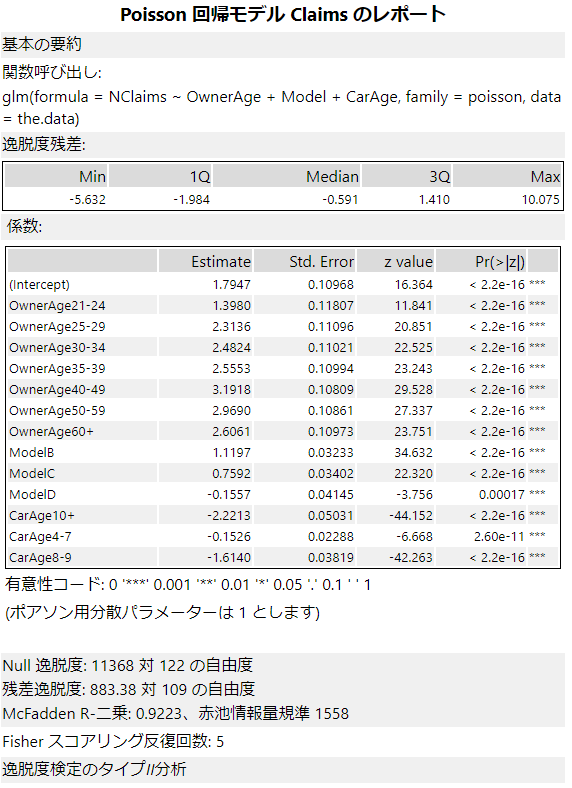
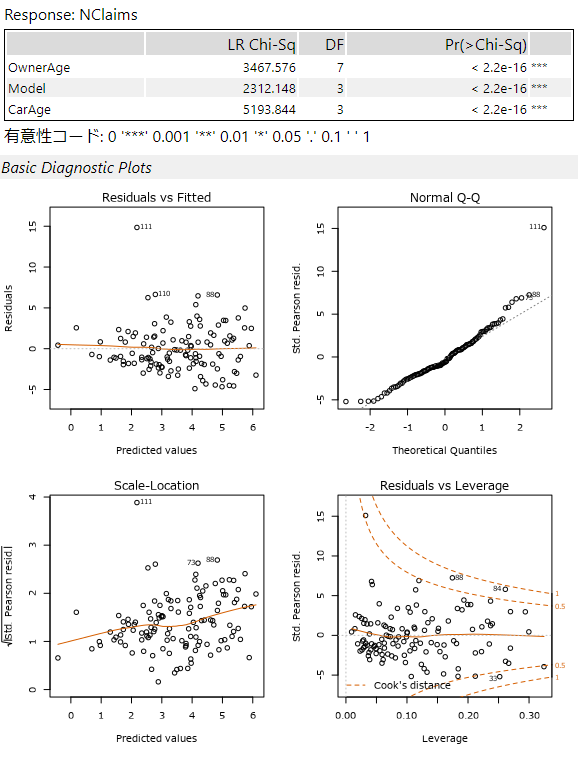
結果を読み解く
いずれもガンマ回帰と同様の項目ですのでここでは省略します。使っているRの関数は「glm」で、ガンマ回帰と同じです。違いは、familyというオプションをpoissonとすることでポアソン分布のモデルとなっています。
参考URL
Alteryxのツールマスタリーシリーズです。線形回帰ツール。
線形回帰ツールにおいてAlteryxバージョン11で変更された点について記載されています。
クロスバリデーションの機能について書かれたAlteryx公式の情報です。
線形回帰、ロジスティック回帰で使用できる「正則化回帰を使用する」オプションについてのAlteryx社の公式の情報です。
回帰分析の1ページ目の用語について説明が記載されています
一般化線形モデルについての解説(ガンマ回帰、ポアソン回帰で使用されているRの関数がGLM)。
ガンマ回帰、ポアソン回帰で使用されているZ値に関しての説明(Z値はパラメータ0の場合のWald検定であるため)。


コメント