※過去記事はこちら。AlteryxユーザーのためのAdvent of Codeの始め方、1日目、2日目、3日目、4日目、5日目、6日目、7日目、8日目、9日目、10日目、11日目、12日目。

第拾参話 「Point of Incidence」
タイトルは「入射点」。鏡の問題なので・・・。
前回の問題で、無事にスプリングは発見できたようで、溶岩のところに来ることができたようです。しかし、そこには溶岩を見ることはできず、灰と岩ばかりで、鏡で阻害されているとのことです。
ここに鏡の迷路を抜けるための地図があります(入力データ)。灰はドット「.」、岩は「#」です。この地図の中のどこに鏡があるかを見つける必要があります。MAPはいくつかに分割されており、以下の例では2つのマップが途中の空白行で別のものとして分割されています。
#.##..##.
..#.##.#.
##......#
##......#
..#.##.#.
..##..##.
#.#.##.#.
#...##..#
#....#..#
..##..###
#####.##.
#####.##.
..##..###
#....#..#鏡は、それぞれのマップに対して、上下、もしくは左右に一枚配置されています。例えば上の方であれば、
123456789
><
#.##..##.
..#.##.#.
##......#
##......#
..#.##.#.
..##..##.
#.#.##.#.
><
123456789となっており、5列目と6列目の間に存在しています。5列目と6列目が同じ、4列目と7列目が同じ、3列目と8列目が同じ、2列目と9列目が全く同じパターンです。1列目は本来10列目の反射になりますが、10列目はないので無視してオッケーです。
2つ目のマップを見てみると、
1 #...##..# 1
2 #....#..# 2
3 ..##..### 3
4v#####.##.v4
5^#####.##.^5
6 ..##..### 6
7 #....#..# 7となっています。この場合は、4行目と5行目の境に鏡があります。
鏡が存在している行もしくは列の場所を取得します。鏡が横向き(行)に存在しているときは行数×100とします。縦向き(列)に存在しているときは、列数を取得します。パズルの解答はこの行数×100+列数を合計したものになります。
上のサンプルであれば、1つ目が5、2つ目が4×100なので合計で405となります。
Part2は、鏡に一点だけ汚れがあるとのことで、反射の際にどこか一箇所だけパターンが反転していても、そこは汚れなのでそこに鏡がある、ということになります。
・ネ
・
・タ
・
・バ
・
・レ
Part1、2を解いてみる
鏡を探すために、どのようなロジックを組むかがポイントです。非常に様々な方法があるようです。
まず初期のデータを作りましょう。今回は以下のようなデータとしました。
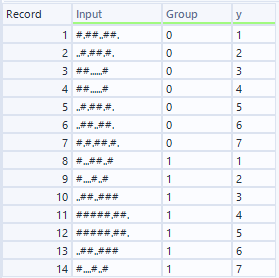
反射かどうかは、例えば、上のインプットの3行目と4行目の間に鏡があるとすれば、鏡の位置で上下にレコードを分けたときに、まず下半分の並びを反転させます。その上で、上半分、下半分を上から並べてInputがすべての行で一致すればそれが鏡の位置だった、ということになります。つまり以下のような判定を行います。
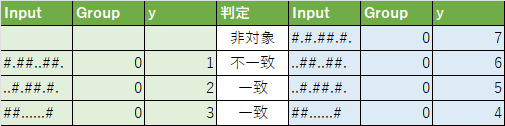
この判定をするロジックをマクロで作り込んでいます。この区切り位置を一つずつ変えていって、最初に合致したものを鏡の位置、としています。
自分の場合は、並びを調整して一致するかどうか、というのを判定するように作りました。
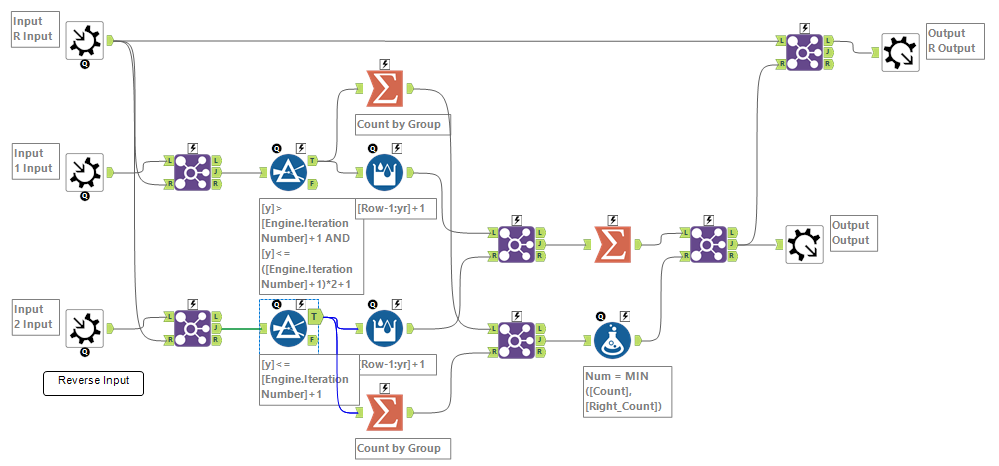
なお、最初は縦に検索し(y軸のどこに鏡がいるか)、その後横(x軸のどこに鏡がいるか)に検索するようにしています(データの持ち方的に縦からやった方が一手減らせるため)。基本的にデータの持ち方を変え、同じマクロ(ロジック)で処理を行っています。
つまり、元のデータを以下のように組み替えるだけで同じマクロが適用できます(マクロで適合するように、フィールド名はxからyに変更してからマクロに突っ込んでいます)。
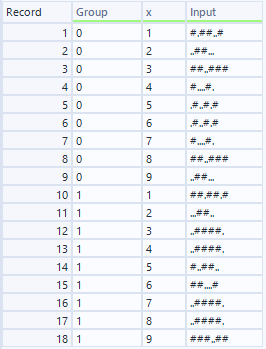
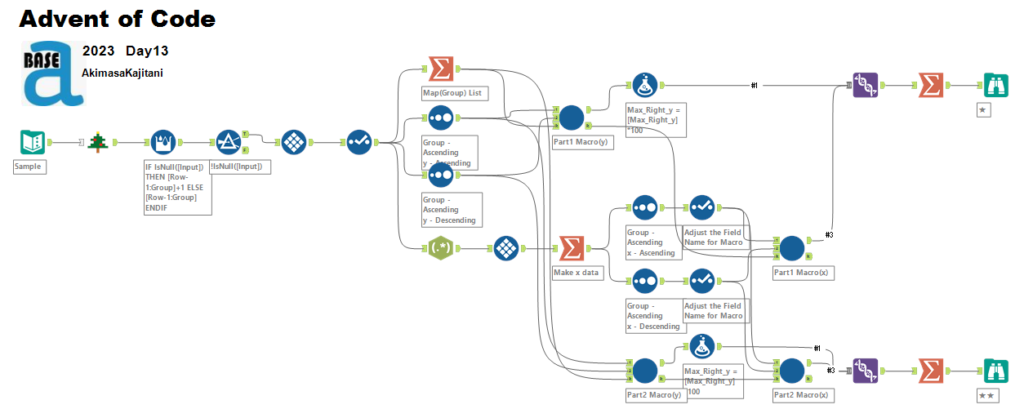
基本的には総当たりで、上から検索していっています。ワークフローとしては以下のとおりです。
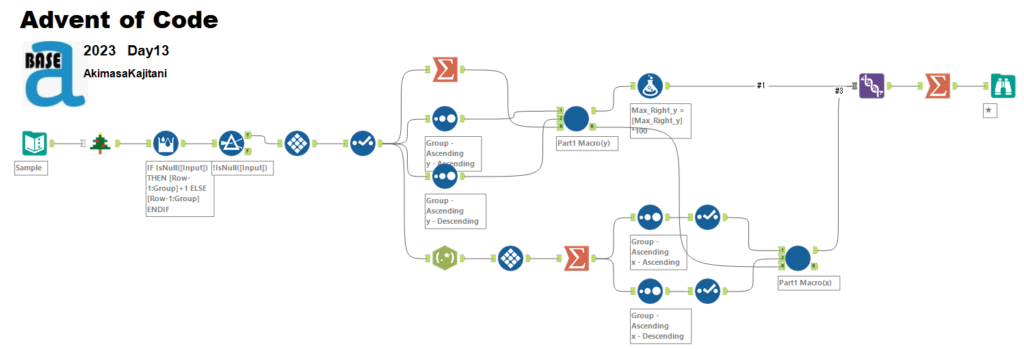
Part2は、一箇所だけ違っていてもOKと判定すれば良いです。ただ、わざわざ一箇所ずつデータを反転させるやり方は時間がかかるため、一致する箇所が一箇所だけ少ない場合に鏡の位置として判定させるようにマクロを作り替えました。
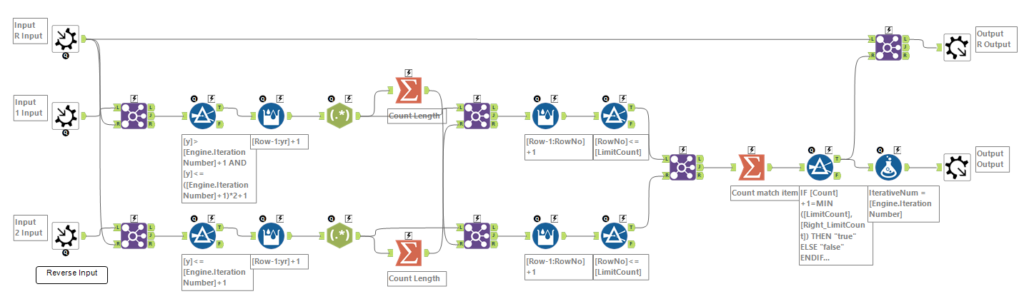
真ん中くらいにあるフィルタツールのところで、以下のようなデータを得ます。
上側のデータストリーム:
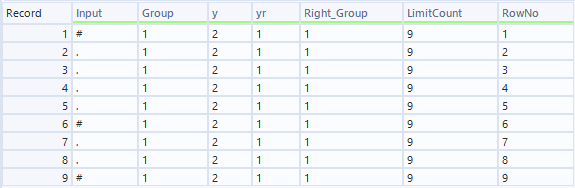
下側のデータストリーム:
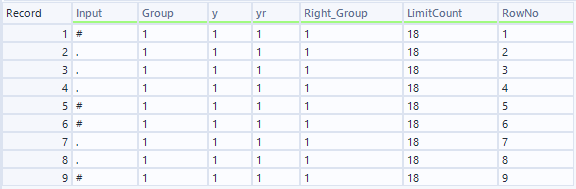
見た目でわかりますが、いずれも上から5行目のみ異なっており、その他は同じです。このデータを結合ツールで結合します(InputとGroupとRowNoで結合します)。
すると、Inputが一つだけ異なっているため、フルセットの数であるLimitCountというものとマッチした件数が一つ差であれば、汚れがそこにあるので、鏡の位置が特定できる、ということになります。
ちなみに、件数が同等であればPart1でもこのマクロは使えます。
まとめ
- 問題文の理解をするのに若干かかったのと、ロジックをどう組み立てるのが良いのか、というとことで少し悩みました。Part2は、汚れの位置がランダムであることにあとから気づき時間を無駄にしました。Part2のやり方の方が時間がかかるので、軽くできる方法でやりましたが、結果的にはPart2マクロを最初から作っていればPart1からすぐクリアできたなぁ、という結論です(まぁ、結果論)。また、高速化のために、反転した並びのデータは予め先に作っています。おかげで、Part1,2あわせて1.5秒で回りました。
- Private LeaderボードでPart1は2位、Part3合わせると3位となりました。1位の人とは15秒差・・・。おしい。全体では約2時間かかりました。やはりPart2で悩みますよね。最初は一箇所ずつ入れ替えていく?って思いましたが、面倒だったのと今の方法をひらめいたのでそのままいけました。さすがにこのレベルだと一時間以内に解くのは結構苦しいですね・・・。


コメント