※過去記事はこちら。AlteryxユーザーのためのAdvent of Codeの始め方、1日目、2日目、3日目、4日目、5日目、6日目、7日目、8日目、9日目、10日目、11日目、12日目、13日目、14日目、15日目、16日目、17日目、18日目、19日目、20日目、21日目、22日目。
23日クリア時点のスクショがないため25日時点のスクショです。
第弐拾参話「A Long Walk」
タイトルは「長い散歩」。確かに長い散歩をする問題でした。
前回大量の砂を作ったため、水のろ過ができるようになりエルフたちは水のろ過作業に入りました。その後滝からおろしてもらい雪の島に到着しました。しかし、水は空気に吸収されています。湿気がたまるまで散歩することになったようです。
散歩コース(パズルのインプット)は、以下のようなマップになっています。「.」は小道、「#」は森林、その他急な坂道があります(^、>、v、<)。スタート地点は左上の端っこの枠外に接した小道です。ゴールは右下の枠外そばの小道です。
#.#####################
#.......#########...###
#######.#########.#.###
###.....#.>.>.###.#.###
###v#####.#v#.###.#.###
###.>...#.#.#.....#...#
###v###.#.#.#########.#
###...#.#.#.......#...#
#####.#.#.#######.#.###
#.....#.#.#.......#...#
#.#####.#.#.#########v#
#.#...#...#...###...>.#
#.#.#v#######v###.###v#
#...#.>.#...>.>.#.###.#
#####v#.#.###v#.#.###.#
#.....#...#...#.#.#...#
#.#########.###.#.#.###
#...###...#...#...#.###
###.###.#.###v#####v###
#...#...#.#.>.>.#.>.###
#.###.###.#.###.#.#v###
#.....###...###...#...#
#####################.#傾斜は一方通行になっています。Part1ではスタートからゴールまでの再長距離(歩数)を調べます。
Part2は、、、斜面もそれほど滑りにくいわけではなく、坂道も登れるようです。この条件での最長の歩数を調べます。
・ネ
・
・タ
・
・バ
・
・レ
Part1,2を解いてみる
Part1は、単純に反復マクロで一歩ずつ歩かせるだけです。分岐地点で全パターンのルートを作っていきます。そのため、徐々にデータが増えていく形になります。
反復マクロは非常に素直なマクロになっています。インプットは、反復用のルート用データと、MAPは読み出し専用にしています。
ルート保存用入力:

現在位置のx、y座標、ゴールの座標、ルート保存用の「Route」です。
MAP:
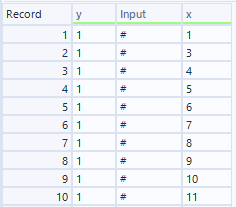
これ、よくよく考えたら「#」抜いて作ったほうがスピードは高速化されますね、、、
反復マクロ:

ワークフロー全景です。
Part2は、坂道のおかげでパターンがあまり増えていなかったところがかなりのパターンになるためレコード数が増えすぎ時間がめちゃくちゃかかるようになってしまいます(いつものデータ量爆発です)。
今回は、ルートの圧縮を行うことで単なるグラフ問題に落とし込むことができます(とはいってもパターン自体は多いですが、反復回数を圧倒的に減らすことができるため、現実的な時間で答えを出すことが可能です)。
最初この圧縮方法に悩みましたが、交差点をノードと考えた時、交差点は周囲の点と3箇所以上で結合できるわけなので、交差点だけ抜き出すことは容易です(スタートとエンドのノードも周囲の点とは1箇所のみで結合できます)。その後、全ノードに対して元のマップで検索を行い、各エッジの長さを出します(これがノード間の距離になります)。あとは、ダイクストラ法でも幅優先探索(Breadth First Search=BFS)でもお好きにどうぞ、ということになります。
Part2では、まずマップから出発します。Part1のワークフローのタイルツールの次のセレクトから分岐します。そこからノードごとに接続される他ノードの数をCountしたものを作ります。Countが1と3位上のものをNodeでTrueとしています。
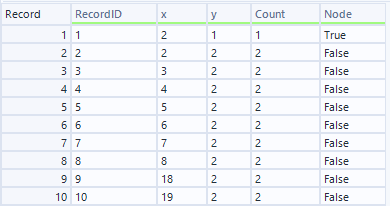
ワークフローとしては以下の通りで、ここまでは特にマクロは不要です。
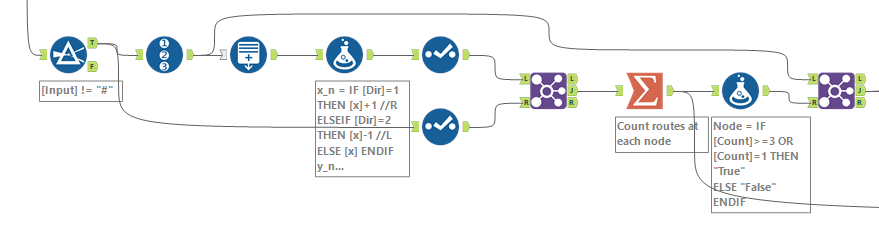
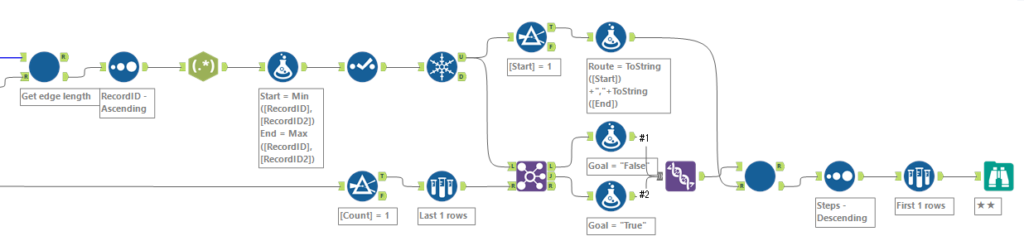
ノード間の移動にかかる時間(Steps数)を取得するために、、、ここはマクロです。先程のデータと、ノードのみのリストを使って、各ノードからマップを辿って行って次のノードになるまで検索を続ける反復マクロを作ります。

ワークフローとしては以下のような感じです。
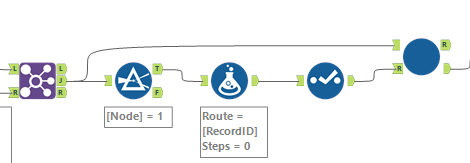
これにより以下のようなデータが得られます。
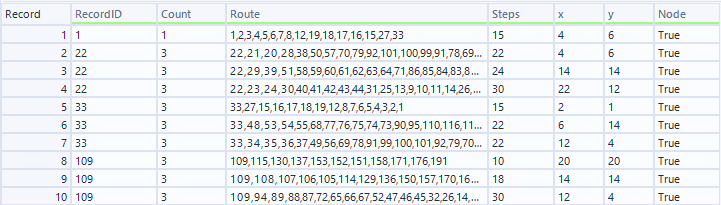
RecordIDがノードの名称、隣接ノードは、Routeの最後の番号です。これを、最初のPart1のマクロと同じように、幅優先探索(BFS)を行います。
入力は、ルート情報、

そして、マップ(ノード情報)です。
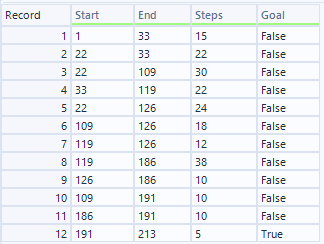
マクロはこちら。比較的シンプルです。
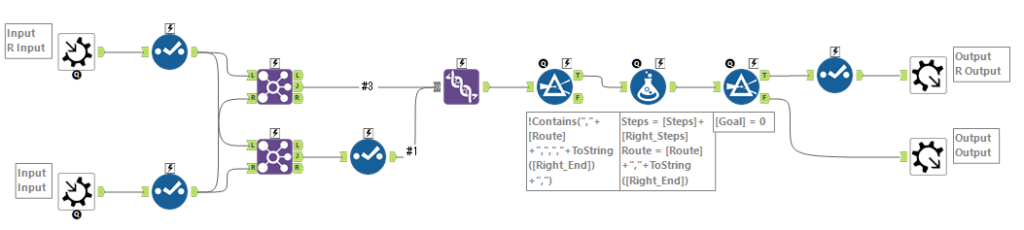
ワークフローは以下の通り。
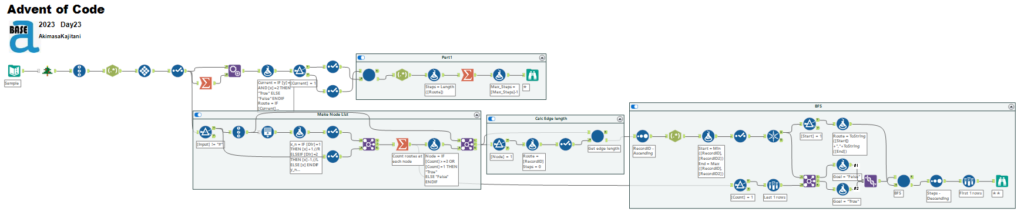
ワークフローの全景です。結構大作ですね!
まとめ
- Part1は比較的素直な問題かと思います。マクロを作るスピード勝負な問題です。
- Part2は、グラフ理論に落とし込めることに気づくかどうかがポイントです。これに気づかないとブルートフォースになるわけですが、解けないわけではないと思いますが、非常に時間がかかります。
- Private Leaderボードで、Part1は6位、Part2は5位となりました。この日は用事が別にあったので、リアルタイム参加できなかった日です。



コメント