Alteryx Predictive Master資格取得を目指すシリーズです。
ARIMAツール

ARIMAモデルは、英語では「AutoRegressive Integrated Moving Average」という長ったらしい名前の頭文字を取って「ARIMA」となっています。これの原型となるのが、AR(自己回帰)、MA(移動平均)モデルで、これを組み合わせて一般化(Iの部分)したモデルがARIMAです。
このモデルは、季節性の強いデータに向いています。
また、ARIMAモデルは、共変量(Covariate)を用いた予測が可能です。これは、線形回帰などの機械学習モデルにあるような特徴量を用いた予測です。共変量を用いてモデルを作成した場合は、予測する際に時系列共変量予測ツールを用いる必要があります(また、時系列比較ツールは使えません)。
設定
必須パラメーター
必須パラメーターの設定は、モデル名、ターゲットフィールドを選択、ターゲットフィールドの頻度が必須となります。
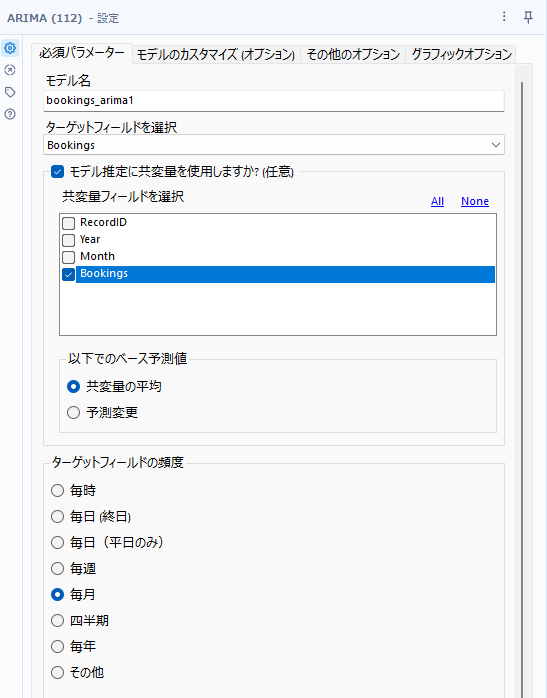
その他の設定として、「モデル推定に共変量を使用しますか?」のオプションにて共変量が設定可能です。共変量を使う場合は、共変量として使用するフィールドを選択する必要があります(このサンプル設定は適当にチェックを入れています。
モデルのカスタマイズ
ARIMAモデルの細かいカスタマイズはこのタブで行います。主に、「自動モデル作成」のカスタマイズと、「完全ユーザー指定モデル」といった形でのカスタマイズの二種類が可能です。デフォルトでは「自動モデル作成」が行われます。
自動モデル作成に使用されるパラメーターをカスタマイズする
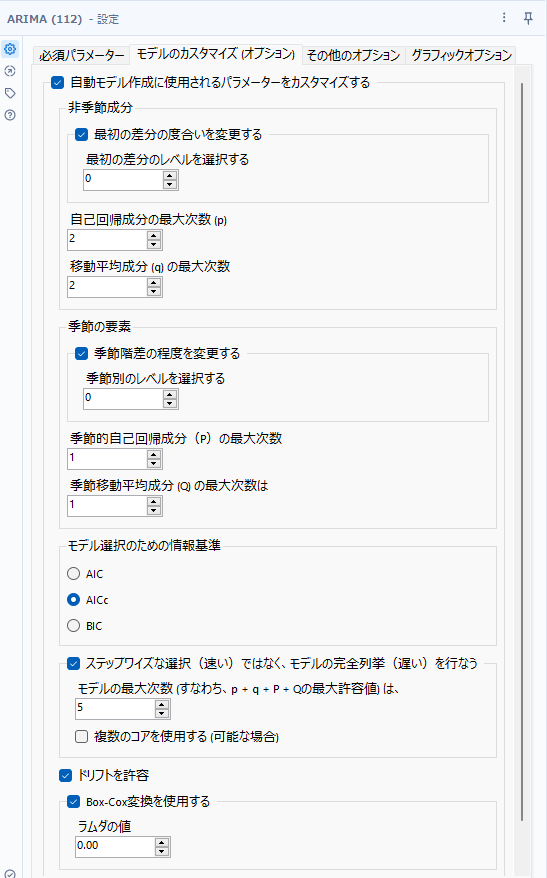
ARIMAモデルは、非季節ARIMAと季節ARIMAと組み合わせられているようなモデルです。
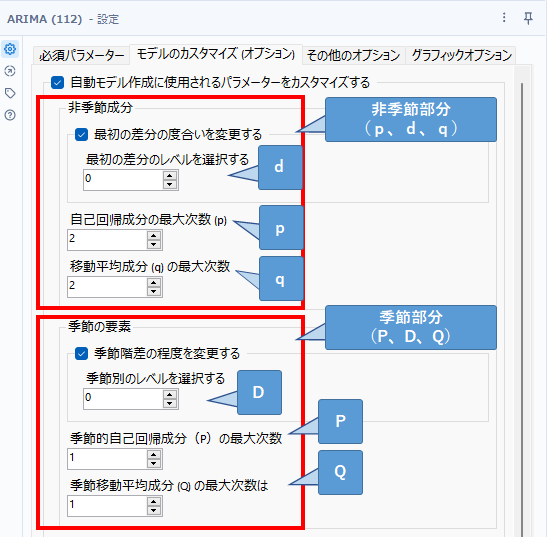
ARIMA(p、d、q)(P、D、Q)
という表記がされますが、前半の(p、d、q)は非季節、後半の(P、D、Q)は季節部分となります。上記のオプション非季節成分は(p、d、q)のカスタマイズ、季節の要素は(P、D、Q)のカスタマイズとなります。
モデル選択のための情報基準
デフォルトではモデルの選択にはAIC(赤池情報量規準)を使用しますが、AICcやBICを使用するように変更することも可能です。
ステップワイズな選択ではなく、モデルの完全列挙を行なう
デフォルトでは、モデルの選択にはステップワイズアルゴリズムを使って行いますが、すべてのモデルを推定して比較することもできます。ステップワイズを使えば、少ない計算量で良好な結果が得られますが、最も良いモデルを発見できるわけではありません。この機能をonにすると、すべての可能なARIMAモデルを実行することで、計算量は増えますが最高のモデルを得ることができます。またこの時、「複数のコアを使用する」オプションを使用するとPCの余っているCPUコアを使うことができます。
ちなみに、ステップワイズ法では結構外す場合もあるようなので、完全列挙も良いかもしれません。
ドリフトを許容
チェックをつけると定数項を許容します。全体平均が0である確信がある場合はチェックを外してください。一般的には定数項を含めます。
Box-Cox変換を使用する
チェックを入れると、ターゲットフィールドのBox-Cox変換を実行できます。ユーザーはラムダの値(0~1)を指定可能です。
Box-Cox変換:データの分布を正規分布に近づけるための変換
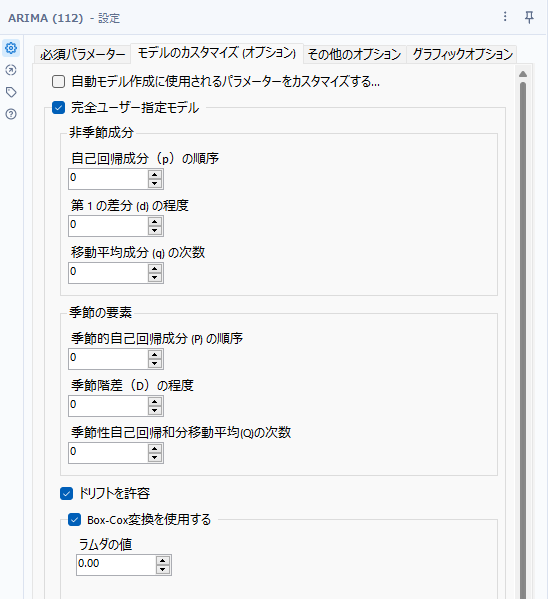
完全ユーザー指定モデル
完全にユーザー指定のモデルを作成したい場合はこちらのオプションを使います。
その他のオプション
基本的なモデルのカスタマイズです。可能であればシリーズ開始期間を指定しましょう。
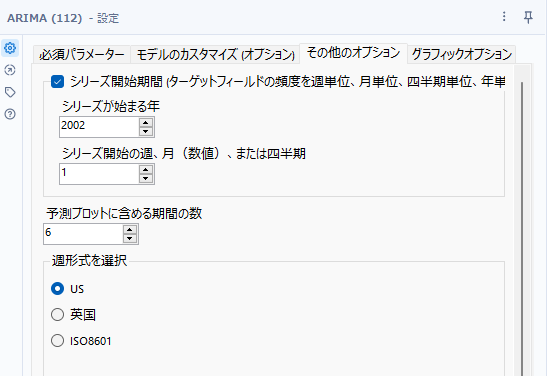
シリーズ開始期間
レコードの最初のデータの年と週/月/四半期の指定が可能です。これを指定すると、結果がちゃんと年で出てくるため非常に結果が見やすくなります。ただし、ターゲットフィールドの頻度を毎時、毎日(終日)、毎日(平日のみ)にしていると指定できません。
予測プロットに含める期間の数
予測精度を検証するための予測期間を指定します。デフォルトは6です。最終的な予測期間は、時系列予測ツールで指定します。
週形式を選択
年の最初の週と、週の始まりの曜日を指定します。
- US:週の最初の日は日曜日
- 英国:週の最初の日は月曜日
- ISO8601:週の最初の日は月曜日
出力結果
メソッド
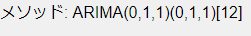
メソッドは、使われたモデルが記載されます。通常ARIMAモデルはAICの値を使って最適なモデルを作成します。AICが同程度の場合は、誤差を計算して優れたモデルを使用します。カスマイズで行った場合はそのモデルが記載されます。
ここでは、ARIMA(0,1,1)+Seasonal(0,1,1)ということになります。最後の[12]は周期です。
関数呼び出し
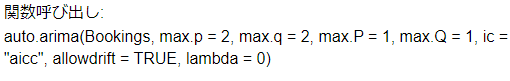
ARIMAツールが内部で呼び出したRの関数のオプション等が記載されます。
係数
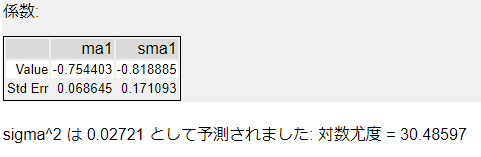
係数の項目は、ARIMAで選択されたモデルによって出力が変わります。
sigma^2は観測値と予測値の残差の標準偏差です。これが小さいほど良いモデルということになります。また、対数尤度(log likelihood)はARIMAモデルがモデルをフィッティングする際にこれを最大化するようなパラメータを推定しています。そのため、大きいほど観測値をよく説明できているということになりますが、モデルの比較については次に出てくる情報規準を使用します。
情報基準
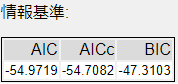
- AIC(Akaike Information Criterion):赤池情報量規準
- AICc:補正赤池情報量規準
- BIC(Bayesian Information Criterion):ベイズ情報量規準
これらの値は、統計モデルの良さを評価するための指標ですが、小さい方が良いです。
サンプル内エラー測定

作成したモデル内での予測値と実際の値の誤差です。
- ME(Mean Error):平均誤差
- RMSE(Root Mean Squared Error):二乗平均平方根誤差
- MAE(Mean Absolute Error):平均絶対誤差
- MAPE(Mean Absolute Percentage Error):平均絶対パーセント誤差
- MASE(Mean Absolute Scaled Error)平均絶対スケール誤差
- ACF1(Autocorrelation Function at lag 1):ラグ1自己相関
ACF1は、各レコードと一つ前のレコードとの相関となります。これが大きい場合は、直前の値の影響を強く受けるということになります。
ME~MASEは基本的に絶対値が小さい値が望ましいです。
モデル残差のLjung-Box検定
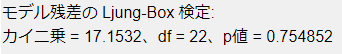
リュング・ボックス検定は、時系列の自己相関の集まりが0と異なるかどうか、に関する統計的検定です。つまり、自己相関の有無を確認できます。p値が0.05未満であれば自己相関があり、それ以上の場合は有意な自己相関があるとは言えない、ということになります。
基本的に自己相関を持っていないことが好ましいため、p値が0.05未満の場合はモデルの見直しを推奨します。
プロット
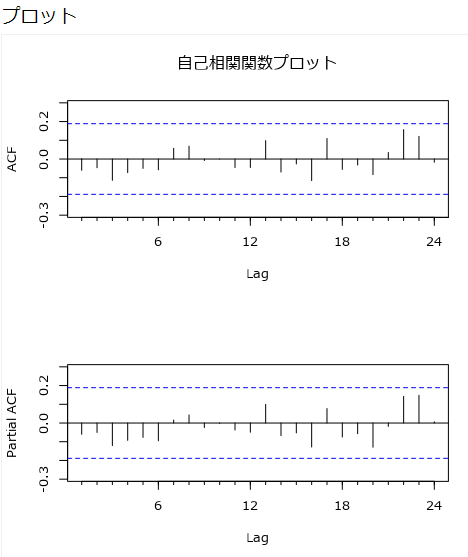
ACF(Autocorrelation Function)プロット
ACF(Autocorrelation Function)=自己相関のプロットは、観測値と過去の値の間の相関を示します。縦軸は相関係数、横軸はラグ数(遅れ)となります。
ラグ1後の有意性が小さく(0に近いということ)、平均、分散が変化しないのであればデータは定常ということになります。定常であるということは、将来も同じであるということで安定した予測モデルであるといえます。
相関がゼロ相関に向かってゆっくりと減衰するような場合、データは定常ではありません。この場合は差分が必要です。差分は、平均と分散が一定になるまで、各値を前の期間の値で減算する方法です。季節ごとの差異については、複数行フォーミュラツールで、例えば[Sales]-[Row-12:Sales]といった式を用いて12ヶ月の年間シーズンを表すようにします。
相関が青の点線を超える場合は、有意であるということになり、繰り返しパターンは季節性を示します。
Partial ACFプロット
部分的自己相関プロットは、以前のすべてのラグ期間の値を制御しながら現在の期間とラグ期間の間の相関を示します。
PACFがラグ1の後に低下し、定常系列がラグ1で正の相関を持つ場合、AR項が最適です。PACFがラグ1の後、緩やかに低下し、定常系列がラグ1で負の相関を持つ場合、MA項が最適です。
Forcasts from ARIMA
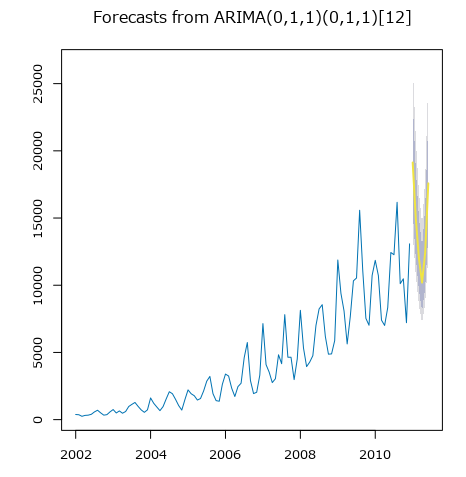
このグラフは、青が実測値で、黄色が予測値です。灰色は信頼区間です。
参考
ナレッジベースのARIMAの記事です。
Rの予測パッケージを使った時系列予測のオンライン教科書です(英語)。日本語訳も出ています。

コメント