Alteryx Predictive Master資格取得を目指すシリーズです。
指数平滑法（ETS）ツール
指数平滑法（ETS）ツールは、英語ではExponential Smoothingと呼ばれる手法ですが、ETSはError Trend Seasonalityの略です。
このモデルは、過去のデータのうち、新しいデータに重みをおき、過去データには、古いほど指数関数的に影響が少なくなるようなウェイトをかけて移動平均を計算し、将来を予測するモデルです。また、レベル、トレンド、季節性という3つの時系列コンポーネントを考慮できます。
なお、最近のデータに依存するパターンを持つデータに向いています。
設定
必須パラメータ
必須となる設定は、「モデル名」、「ターゲット・フィールドの選択」および「ターゲット・フィールドの頻度」（レコードの間隔）です。
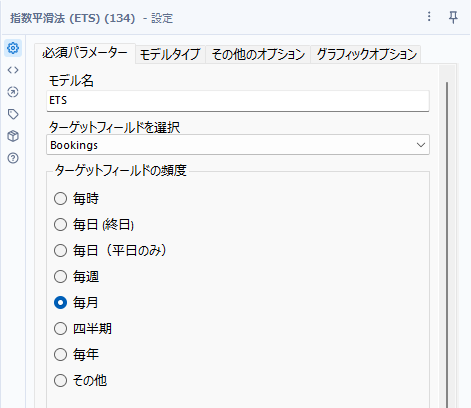
ターゲットフィールドの頻度については、特に日付型のフィールドなどを指定しないため、厳密にここで指定した間隔になっている必要があります。これは、時系列フィルツールなどを使って予め確認しておく必要があります。
モデルタイプ
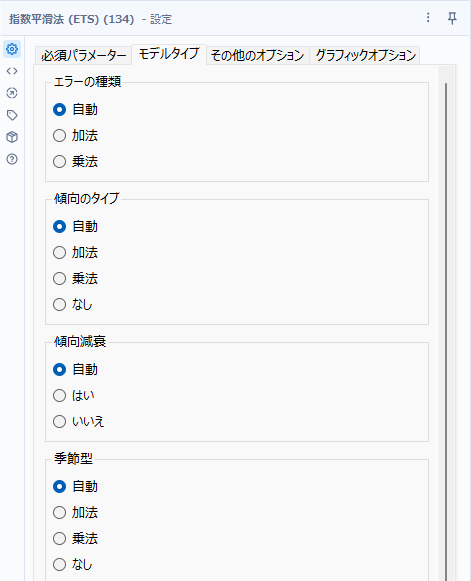
基本的にETSはすべて自動設定があるので、まずは自動で進めてかまいません。ここで選択したパラメータによって内部で呼び出しているRのETSモデルの詳細なモデルが決まります。自動とした場合の結果は、R出力のレポートの「メソッド」で確認できます。
その他のオプション
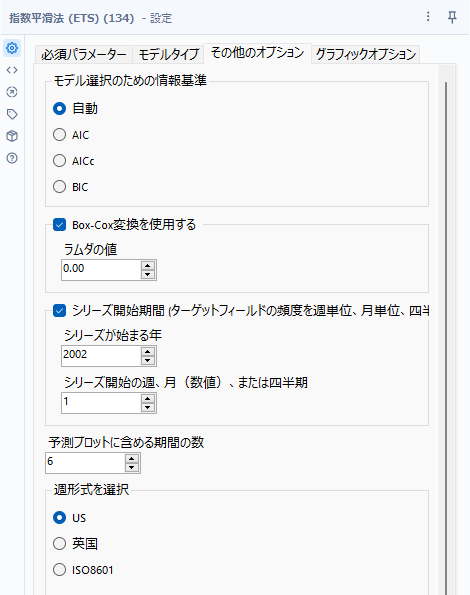
モデル選択のための情報基準
自動、AIC（赤池情報量規準）、AICc（補正赤池情報量規準）、BIC（ベイズ情報量規準）から選択可能です。モデルタイプで自動とした際、ここで選択した規準の値が最も小さくなるモデルを選択します。ここで自動とした場合は、ターゲットの観測値が48以下であればAICc、それ以外ではAICが使用されます（ヘルプより）。
Box-Cox変換を使用する
チェックを入れると、ターゲットフィールドのBox-Cox変換を実行できます。ユーザーはラムダの値（0～1）を指定可能です。このオプションを使用した場合は、３つの時系列コンポーネントの乗算仕様は考慮されません。
Box-Cox変換：データの分布を正規分布に近づけるための変換
シリーズ開始期間
学習させるデータの最初のデータがいつであるか指定すれば、出力もしっかりと年が記載されわかりやすくなります。ただし、「ターゲットフィールドの頻度」が「毎時」「毎日（終日）」「毎日（平日のみ）」に設定している場合は設定できません。
予測プロットに含める期間の数
予測精度を検証するための予測期間を指定します。デフォルトは６です。最終的な予測期間は、時系列予測ツールで指定します。
週形式を選択
年の最初の週と、週の始まりの曜日を指定します。
- US：週の最初の日は日曜日
- 英国：週の最初の日は月曜日
- ISO8601：週の最初の日は月曜日
出力結果
Decomposition by ETS(M,A,M) method
分解プロットということになりますが、説明の通りです。
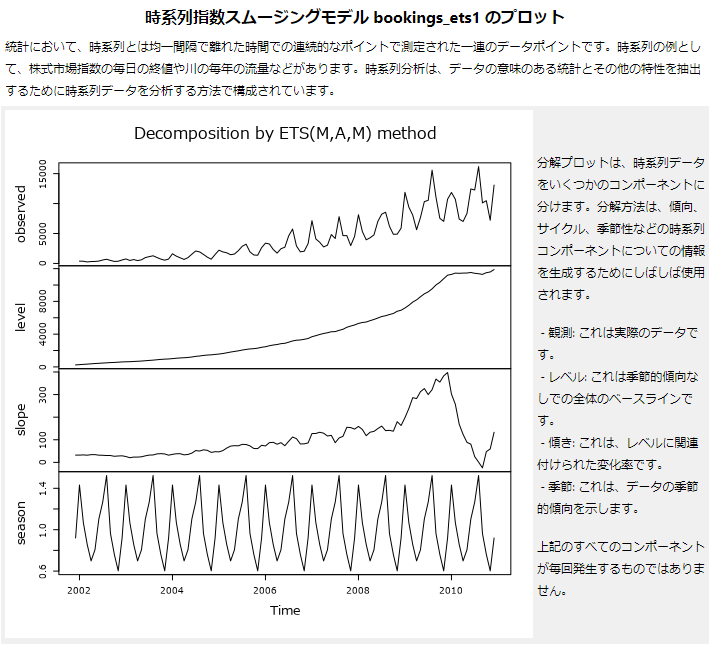
上から、
- observed（観測）：実際のデータ
- level（レベル）：季節的傾向なしの全体的なベースの傾向
- slope（傾き）：レベルに関連付けられた変化率
- season（季節）：季節的傾向
を示しています。
ETS(M,A,M)による予測
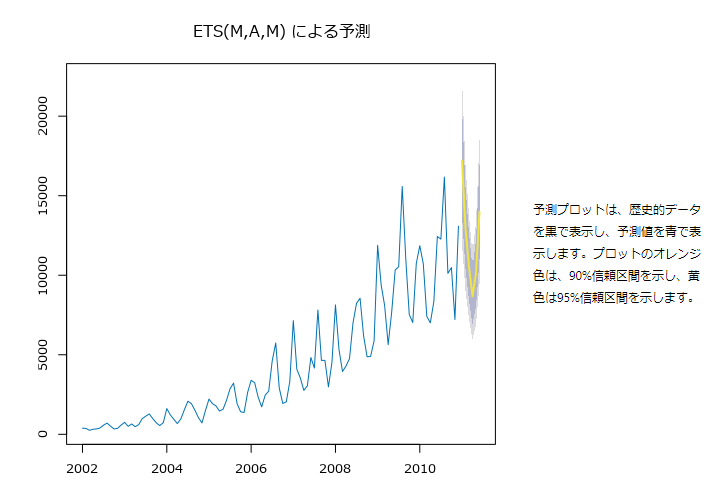
予測プロットの説明文は少し誤っているように思います。インタラクティブ出力では説明に近く、黒が実測、青が予測値ですが、R出力では青が実測値で、黄色が予測値です。灰色は信頼区間です。
レポートの続きは、時系列指数スムージングモデルの要約になります。
メソッド
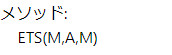
ETSというRの関数を内部的に呼んでいます。カッコ内のパラメータについては１番目は「レベル」２番目が「トレンド」３番目は「季節性」です。M＝Multiplicative（乗法）、A＝Additive（加算）、Ad＝加法減衰、N＝None（なし）です。選択したオプションによって変化します。それぞれのオプションの組み合わせによって内部的なモデルが変化します。
基本的には、情報基準によって自動的に最適なものが選択されるため、自動で問題ないと思われます（裏付けがないためご注意ください）。
サンプル内エラー測定
作成したモデル内での予測値と実際の値の誤差です。
- ME（Mean Error）：平均誤差
- RMSE（Root Mean Squared Error）：二乗平均平方根誤差
- MAE（Mean Absolute Error）：平均絶対誤差
- MAPE（Mean Absolute Percentage Error）：平均絶対パーセント誤差
- MASE（Mean Absolute Scaled Error）平均絶対スケール誤差
- ACF1（Autocorrelation Function at lag 1）：ラグ１自己相関
ACF1は、各レコードと一つ前のレコードとの相関となります。これが大きい場合は、直前の値の影響を強く受けるということになります。
ME～MASEは基本的に絶対値が小さい値が望ましいです。
情報基準
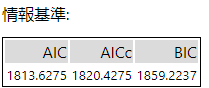
- AIC（Akaike Information Criterion）：赤池情報量規準
- AICc：補正赤池情報量規準
- BIC（Bayesian Information Criterion）：ベイズ情報量規準
これらの値は、統計モデルの良さを評価するための指標ですが、小さい方が良いです。
スムージングパラメーター
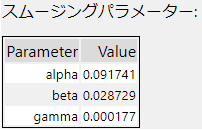
平滑化パラメーターです。関数呼び出しの際に指定も可能なのですが、本ツールでは指定できるようになっていません。ここに表示されている値は推定値です。
alpha：最新の観測値に基づく予測の割合を示します。 データのレベルを表します。
beta：指数関数的減衰のパラメーターです。 通常 0 から 1 の間を取ります。1 に近いほど、最近の観測値の重みが高くなります。 データのトレンドを表しています。
gamma：ガンマが大きいほど、より最近の観測値に重みが置かれます。 データの季節性を表します。 季節性はレベルに比例して増加します。 ベータとガンマの値が小さいと、スロープと季節性の経時変化が非常に小さくなります。
初期状態
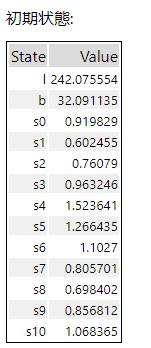
この初期状態は、ホルト・ウィンスター法における初期状態パラメータです。Rでは指定できますがこれも推定値です。
- l：レベルの初期値
- b：トレンドの初期値
- s0～s10：季節性の初期値
参考
ナレッジベースのETSの記事です。
コメント