※過去記事はこちら。AlteryxユーザーのためのAdvent of Codeの始め方、1日目、2日目、3日目、4日目、5日目、6日目、7日目、8日目、9日目、10日目、11日目、12日目、13日目
14日目です。トップの画像は25日まで完走したものを使っています・・・。
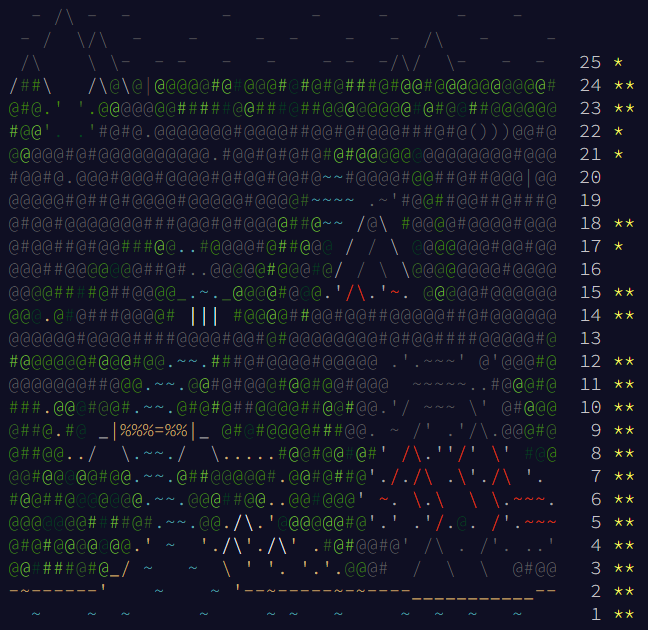
タイトルは、「Regolith Reservoir」です。レゴリス貯水池??
今回の問題は、洞窟に砂が落ちていく問題です。
サンプルの入力データとしては、以下のようになっています。
......+...
..........
..........
..........
....#...##
....#...#.
..###...#.
........#.
......o.#.
#########.「+」が砂の落ちてくる発生元。「#」は壁。「○」は砂粒です。「.」はなにもない空間を示しています。
砂は「+」からまっすぐ直線的に落下しますが、落ちている砂もしくは壁に当たると、まず、左下に落ちることができるか判定し、落ちることができれなければ右下に落ちようとします。どちらも落ちることができなければそこでストップします。
基本的なルールはこれだけです。
Part1では、最終的には以下のようにずっと落ち続けるようになります。このときに、どれだけの砂が静止するかカウントを数えます。つまり、以下のようになった際に、○の数を数えます(「~」は、流れる砂を示します。
.......+...
.......~...
......~o...
.....~ooo..
....~#ooo##
...~o#ooo#.
..~###ooo#.
..~..oooo#.
.~o.ooooo#.
~#########.
~..........
~..........
~..........
Part2では、与えられた障害物の下2行をあけて床が存在することがわかりました。このときに、砂の出現場所が埋もれて完全にすべての砂が流れない状態(停止状態)になった際の砂のカウントを求めます。Part2では非常に多くの砂が貯まるようになっています。つまり、以下のようなイメージです。
............o............
...........ooo...........
..........ooooo..........
.........ooooooo.........
........oo#ooo##o........
.......ooo#ooo#ooo.......
......oo###ooo#oooo......
.....oooo.oooo#ooooo.....
....oooooooooo#oooooo....
...ooo#########ooooooo...
..ooooo.......ooooooooo..
#########################・ネ
・
・タ
・
・バ
・
・レ
解いてみる
シンプルに砂の動きをシミュレートしましょう。つまり反復マクロで対応します。
入力データは、壁のデータだけなのですが、
498,4 -> 498,6 -> 496,6
503,4 -> 502,4 -> 502,9 -> 494,9といったデータでインプットされます。つまり(x1,y1)→(x1,y2)→(x2,y2)といったラインデータとなっています。このままだと使いにくかったのですべて分解し、ポイントデータにしています。
さらにマクロ内で使うデータは、「#」(壁)、動いている砂、始点、止まっている砂、といくつか分かれているので、「alive」というフラグ格納用の項目を作りました。
これらのデータを使って反復マクロ内で砂の動きをシミュレートしていきます。砂が発生してから真下の最大となるyをまず求め、左下のマスがあいていれば左下に落とします。左下のマスが空いてなければ右下のマスがあいているかどうか見て、あいていれば落とします。どこにも行けなければStopです。ひたすらこれを繰り返します。
ちなみに、入力データを可視化すると以下のようになっていました。
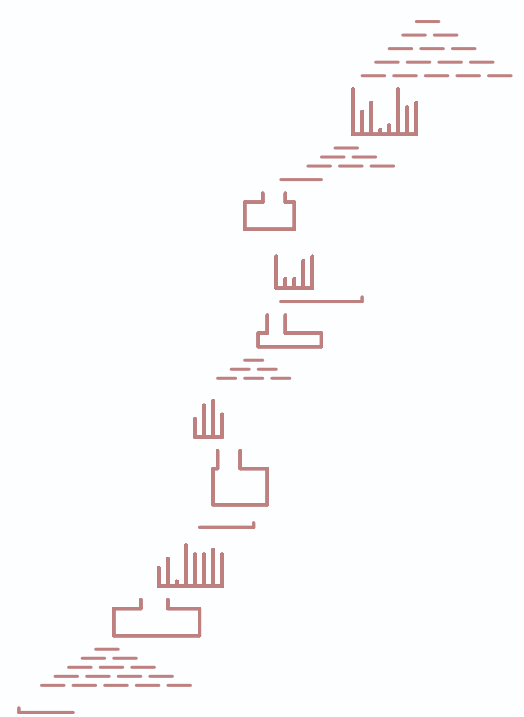
空間ツールを使って可視化すると、見栄えは良いのですがあまりデバッグには向いていないような気がします。自分はx、y座標を知りたかったので、デバッグ用にはテーブル形式で表示し、Excelに貼り付けてデバッグしていました。つまり、以下のような感じでやってました。

Part1のワークフローは以下のとおりです。データをまず整えて、あとはマクロ任せです。

マクロの中身は以下のとおりです。直下、左下、右下のレコードを生成して、結合できるかどうか、といった感じで判定を行っています。つまり、壁や今まで生成した砂と結合した際に結合できると障害物があるので進めない、という判定にしています。

Part1の結果は以下のとおりです。888個の砂粒が生成されました。
Part2は、下に床があり、砂の出てくる出口がうまるところまで行くと何粒の砂が必要か、ということで、どんどん砂が積もっていくようになります。これ、かなりの数になるのですが、最大まで積もったときの砂の数は底辺かける高さ割る2の三角形の面積で求めることができます。そこだけ手計算で求めても、28224粒、とのことなので、900粒で10分くらいワークフローの処理にかかっていたので、かなり時間がかかることは確実です。
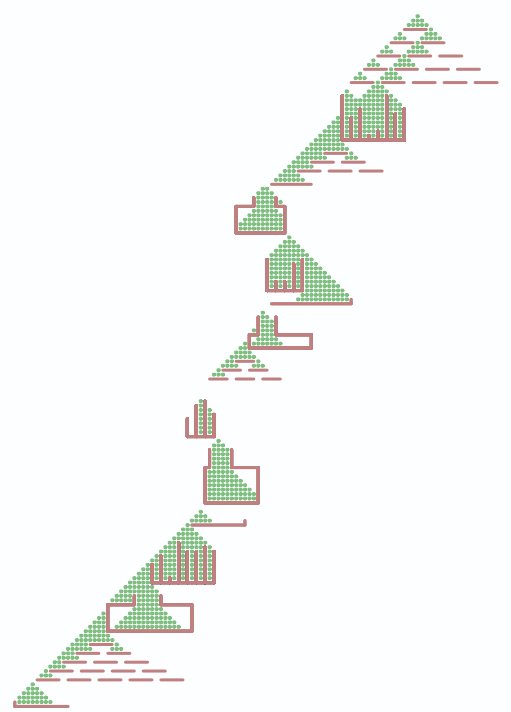
そこで、考えかたを変えました。上の可視化されたものを見ると、砂が積もらない部分があることがわかります。積もらない部分のみシミュレートできれば全体の砂の数から引き算するだけです。ということで、それをシュミレートすることにしました。
つまり以下のようになります(緑の部分が砂が積もらない部分です。1988個分の部分は砂が積もらないということになりました(が、一番低い壁から2マスだけ下に床があるので、左下の方の部分はもう少し数が減ります。

Part2のワークフローは以下のようになります。
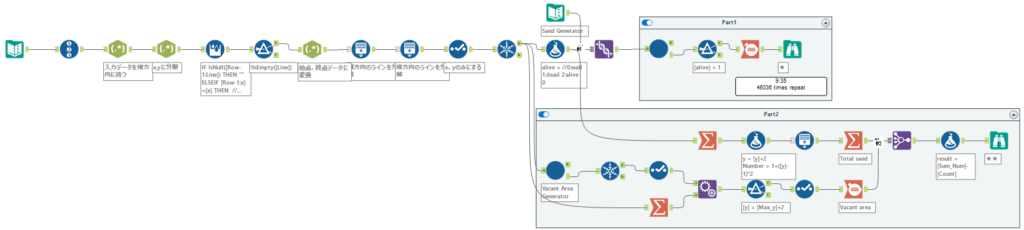
砂粒がふらない部分のシミュレーションマクロは以下のようになります。

Part1より条件的には単純なので比較的シンプルになっています。
まとめ
- 14日目は、図形的な問題です。こういうシミュレート系の問題もちょこちょこ出ます。このような問題のような場合は、シミュレートの結果を可視化できるようにしておくのがデバッグのポイントです。
- Part1も、データ量が多く実際にワークフローを動かすと10分近くかかりました。これは、砂の動きのシミュレートのため、反復マクロが4万6千回動作しているからです。反復マクロにしてしまうと処理的にどうしても遅くなるため要注意です。Part2はデータ量が非常に多くなるため、Part1の延長線だと非常に厳しいです(一応無理やり解けるらしいですが・・・)。考え方を変えることで処理時間は短くなりますが、思いつくのが大変で、完全に解けている人は比較的少ないです。
- 13と同様、非常にみなさん解くのに時間がかかっています。
- 個人タイム:数日にかけて解きました(Private Leaderboardで5位)
※短時間で解けなかったのでゆっくりやっています・・・


コメント