※過去記事はこちら。AlteryxユーザーのためのAdvent of Codeの始め方、1日目、2日目、3日目、4日目、5日目、6日目、7日目、8日目、9日目、10日目
11日目です。
タイトルは、「Monkey in the Middle」。真ん中の猿、ですね。
今日の問題は、無言になるしかないですね・・・。Part1はがんばってできますが、Part2は、Int64がオーバーフローするので何かしら対策が必要な問題です。数学的なトリックを取るか、巨大な数でもなんとか計算できるようにするか・・・。
今回の問題は、数匹の猿が荷物を持っていく、という問題ですが、「心配度」を計算し、その結果で他の猿に荷物を渡してしまう、という問題です。
サンプルの入力データとしては、以下のようになっています。
Monkey 0:
Starting items: 79, 98
Operation: new = old * 19
Test: divisible by 23
If true: throw to monkey 2
If false: throw to monkey 3
Monkey 1:
Starting items: 54, 65, 75, 74
Operation: new = old + 6
Test: divisible by 19
If true: throw to monkey 2
If false: throw to monkey 0
Monkey 2:
Starting items: 79, 60, 97
Operation: new = old * old
Test: divisible by 13
If true: throw to monkey 1
If false: throw to monkey 3
Monkey 3:
Starting items: 74
Operation: new = old + 3
Test: divisible by 17
If true: throw to monkey 0
If false: throw to monkey 1またもやこのデータ整理だけでも、Weekly Challengeだと中級と名乗れます。
Starting itemsというのが荷物です。数値は心配度。Operationは、猿が荷物の心配度に変化を与える計算式です。oldというのは、現在持っている荷物の心配度のことです。Operationを行った心配度に対して3を割って小数点以下は切り捨てします(これが新たな心配度となります)。さらにTestのところにある数値で割り算をして、余りが出たか出ないかでどの猿に荷物を渡すかが決まります(このときのの荷物の心配度は新しい心配度になります)。
つまり上のデータは以下のようにテーブル化するようなイメージでしょうか。
| Monkey No | Item | Operation | Divisible | Throw_True | Throw_False |
| 0 | 79,98 | * 19 | 23 | 2 | 3 |
| 1 | 54,65,75,74 | + 6 | 19 | 2 | 0 |
| 2 | 79,60,97 | * old | 13 | 1 | 3 |
| 3 | 74 | + 3 | 17 | 0 | 1 |
実際の動きとして、上から実行していきます。0番の猿が手持ちの荷物の79と98に対して判定を行って2か3の猿に荷物を投げます。これが1ラウンドです。Part1は20ラウンド行います。
場合によっては手持ちの荷物がなくなったりしますが、最終的には各猿が何回荷物を渡す判定をしたか、という回数をカウントし、上位2匹の猿のカウントを掛け算します。
Part2は、まずラウンド数が10,000回になります。また、心配度を計算するときに3で割りません。これにより値が非常に大きい値になります(具体的に言うと、INT64でさえ超えます)。
・ネ
・
・タ
・
・バ
・
・レ
解いてみる
今回は、二重に繰り返すイメージの問題です。各ラウンドのループと20回もしくは10000回行うループです。
まず、マクロに入れるためのデータを整形していきます。
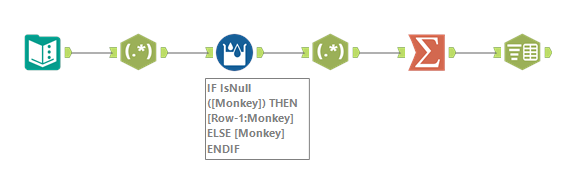
ただ、Itemは常に変更かかりそれ以外の猿のオペレーションは固定なので、別のデータにした方が良さそうです。
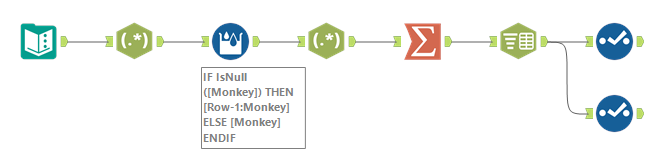
ここからマクロですが、まず完成形こちらです。

まず、外周のマクロです。単に繰り返すだけのマクロで、Part1ならループ回数を20回に指定します。Part2なら10,000回です。
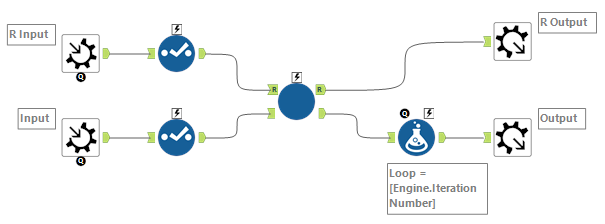
内部マクロです。
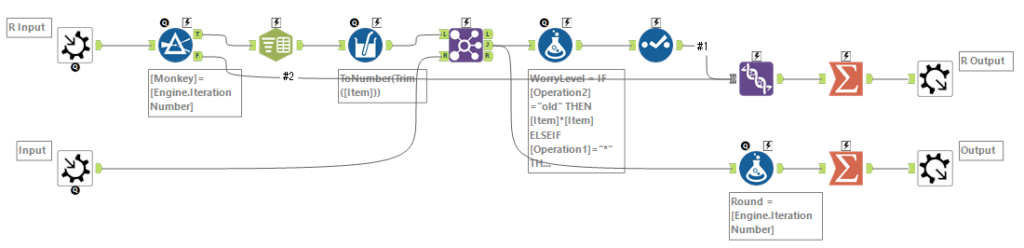
今回、各荷物は「10,20」のような形で保持しているため、マクロ内部で行方向に分割して処理を行う必要があります。もちろん、最初から行方向に分割しておくことでも対応可能です。
ちなみに、Part1はそれほどはまらずデータ成形、2つの反復マクロとロジック作成で1時間取られたという感じです。処理自体は6レコード×20回=120回ループなので速攻終わります。
次に、Part2です。最も厄介なのはこちらです。10,000ループに増えているのでそれなりの時間がかかることはわかっていました。また、内部ロジックとして、心配度を3で割らないので、数値が大きくなることは予想していました。
が、答えが合わず・・・。R出力に出てくる値を見ると、途中からNullになっています。つまりオーバーフローしてNullになっているわけです。
どこかInt32のままのところはないか?文字数を短くしているところはないか?と散々見たのですが間違っていませんでした。
結局、Redditを見てみると数学的なアプローチが必要、とのことでした。
結論としては、Int64を超えないような工夫をする必要があるのですが、最小公倍数(LCM)を使います。つまり今回、猿が誰に渡すか判断のために割り算して剰余を見ているのですが、その割り算している数の最小公倍数を求め、その値と剰余を使ってスケーリングする、ということになるようです。そうすれば、LCM以上の数にならないのため、Int64をオーバーフローしない、ということになります。
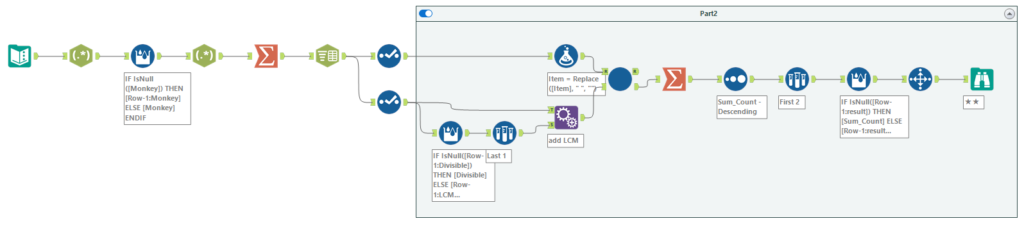
Part2用の外側の反復マクロです。Part1との違いはループ回数だけです。
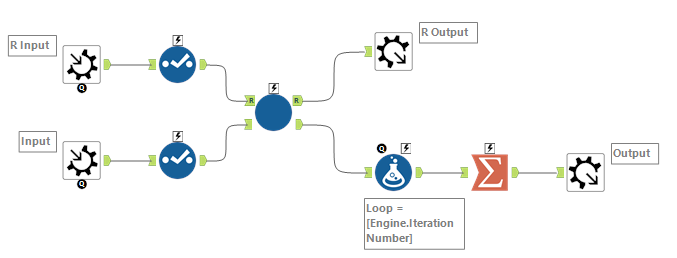
内側の反復マクロです。ループ回数が多いのでデバッグ用の不要なフォーミュラは削除したのと、処理内容軽くするために処理を一部直しています。一番のポイントは3で割らず、LCMでMOD計算しているところです。

Part2は約3分くらい処理にかかりますが、手直しするたびに3分待たされるのはなかなかの苦行ですね・・・(とは言え、昔のプロジェクトで1回し1時間とかもあったので、それ考えたら楽勝ですね・・・)。
まとめ
- 11日目も、Advent of Codeではしばしばあるタイプの問題です(数学的トリックで解ける)。確かに2年前くらい前に中国の剰余定理を使う問題がありましたが、それを思い出します。
- 最速の人で5時間。ここまで来ると実質何時間かけていたかもうわからないですよね・・・。昨日以上に人数が少ないです。また、Part1まで解いたあと止まってる人が多いです・・・。
- 個人タイム:Part1 1時間7分56秒、Part2 7時間14分02秒(Private Leaderboardで4位。Part1では最速取れました!)


コメント