Alteryx Predictive Master資格取得を目指すシリーズです。
Alteryxの予測カテゴリに配置されているモデルについて解説していきます。
今回は分類・回帰両方できる「ニューラルネットワーク(Neural Network)」について解説していきます。
ニューラルネットワーク(Neural Network)概要

ニューラルネットワークは、脳に着想を得たモデルで、層状に編成され、密に相互接続されたノード(ニューロン)で構成されています。
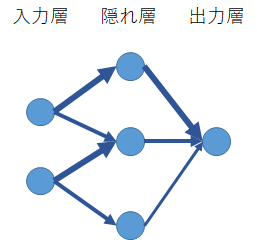
このニューラルネットワークツールは、1つの隠れ層を持ったフィードフォワードパーセプトロンニューラルネットワークモデル(Feedforward Perceptron Neural Network)を構築可能です。
分類、回帰どちらにも対応したモデルです。非線形に向いたモデルです。
長所は以下のとおりです。
- 非線形のデータに対して良いパフォーマンス
- 結果が出るのが早い
- 多重共線性(マルチコ)に耐性がある
一方、短所は以下のとおりです。
- 説明が難しい
- 欠損値に敏感
- 外れ値に敏感
- 学習に時間がかかる
設定
必須パラメータ
必須の設定は、モデル名の決定と、ターゲットフィールドの選択、予測変数の指定となります。
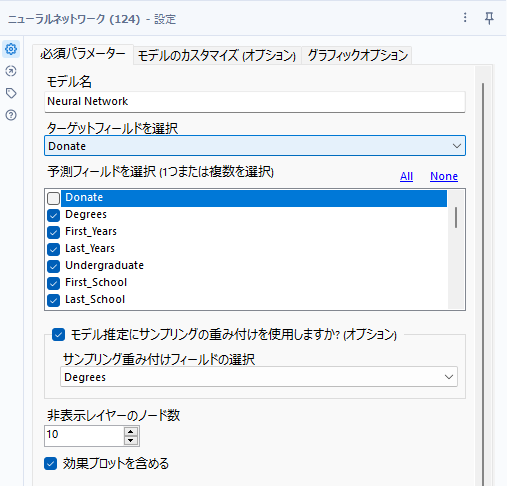
モデル推定にサンプリングの重み付けを使用しますか?
サンプリングする際の重みを持つフィールドを指定することができます。
このオプションは、データセットがサンプリング元の母集団を表していないような場合に役立ちます。
非表示レイヤーのノード数(隠れ層のノード数)
隠れ層に含まれるノード数を指定できるオプションです。値は整数になります。このノード数についての最適値を事前に求める方法はなく、いくつかトレーニングしてみた結果で最良のものを選択する必要があります。少なすぎると、フィッティングが十分ではなくなり、多すぎる場合は、オーバーフィッテイングになります。
デフォルト値は10。最小値は1、最大値は100です。
効果プロットを含める
チェックを入れると、Effectiveプロット(効果プロット)をR出力のレポートに出力します。
モデルのカスタマイズ
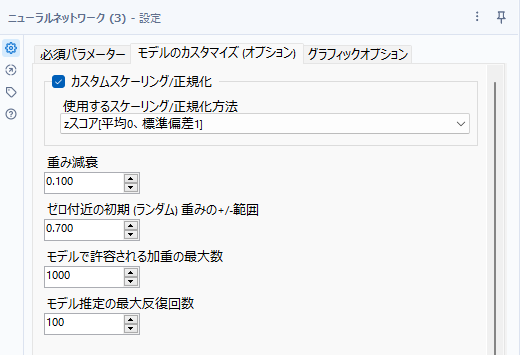
カスタムスケーリング/正規化
入力データ(予測変数)を正規化するオプションです。以下より選択可能です。
- zスコア[平均0、標準偏差1]:平均値を0、標準偏差が1となるように標準化されます。
- 単位区間[0,1]:最小値が0、最大値が1になるように正規化されます。
- ゼロセンタリング[-1,1]:-1~1の間にスケーリングされます。
- スケーリングなし:デフォルト設定です
理論的にはニューラルネットワークモデルのトレーニング時には予測変数の正規化は必要ありません。モデルの重みとバイアスはバックプロパゲーションと呼ばれる手法でトレーニングプロセス中に調整され、各予測変数の大きさに合わせてスケーリングされます。しかしながら、先に正規化しておくことで、モデルのトレーニングがより効率的になることが示されています。
なお、デフォルトではオフとなっています。
重み減衰
推定中の各反復での新しい重み値の動きを制限し、モデルの過剰適合のリスクを軽減するオプションです。この値は0~1の間で設定可能です。大きいとモデルのトレーニング中に可能な重みの調整が制限されます。一般的には0.01~0.2が推奨値とのことです。
ゼロ付近の初期(ランダム)重みの+/-範囲
隠れ層の初期ランダム重みの範囲を制限します。
一般的にはこの値は0.5とされますが、入力される変数の値が大きい場合、より低い値に設定した方が良いモデルになります。
値を0に設定すると、オートで設定されます。設定可能な値の範囲は、0~3です。
モデルで許容される加重の最大数
隠れ層に多数の予測変数とノードがある場合に重要になります。
コード内には許容可能な最大値というものは存在しません。そのため、多くの予測変数と隠れ層のノードがある場合にモデルのトレーニングに時間がかかるケースがあります。加重の数を減らすと、処理速度がアップします。モデルから除外された重みは暗黙的に0になります。
最大値は100,000です。
モデル推定の最大反復回数
アルゴリズムがモデルの重みを相対的に決定する際の改善を見つけるために実行できる試行の最大回数です。
デフォルトでは100です。
重みが改善されなくなった場合は、最大回数より前に停止します。最大値は1,000,000です。
レポートを読み解く
Basic Summary

Call
内部的には、nnet.formulaという関数を呼び出しています。呼び出し時の設定などもCallで確認可能です。
Structure
ニューラルネットワークモデルの構造の概要です。ここで、「58-10-1」とあるのは、入力層-隠れ層-出力層の各層のノード数です。つまり、入力層が58、隠れ層が10、出力層は1となります。重み(weight)は、ノード間の重み付けされた接続です。
Inputs
設定した予測変数です。
Output(s)
ターゲット変数です。
Options
指定したオプションです。ここのEntropy fittingというのは、損失関数です。回帰の場合はLeast-squares fitting(最小二乗法)、多値分類の場合はSoftmax modelingとなります。decayは、重み減衰パラメータに設定した数です。
Final objective funcation value
目的関数の最終的な値です。これが小さいほどモデルの予測精度が高いということになります。
Confusion Matrix(混同行列)
横軸が予測した値、縦軸が実際の値です。

各種プロット
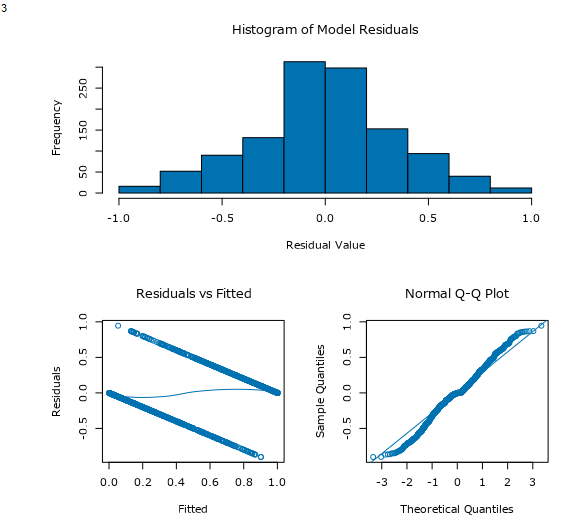
残差(Residuals)は、回帰モデルの場合は、推定値と実際の値の差分となります。分類モデルの場合は、予測値の確率とそのレコードの実際の値の差として計算されます。
Histogram of Model Residuals(モデルの残差のヒストグラム)
残差の出現頻度をプロットしたヒストグラムです。
Residuals vs Fitted
横軸は適合値もしくはレコードがターゲットのクラスに属する確率で、縦軸は残差です。予測値が残差に与える影響を理解するのに役立ちます。
Normal Q-Q Plot
Quantile-Quantileプロットを略してQ-Qプロットと呼びます。ニューラルネットワークの場合、サンプル分位点(推定値の分位点)と理論上の分位点(正規分布など)を比較します。
45度右上に直線上に並ぶのが理想的です。
Effect Plots
必須パラメータにて、「効果プロットを含める」にチェックを入れている場合に出力される効果プロットです。
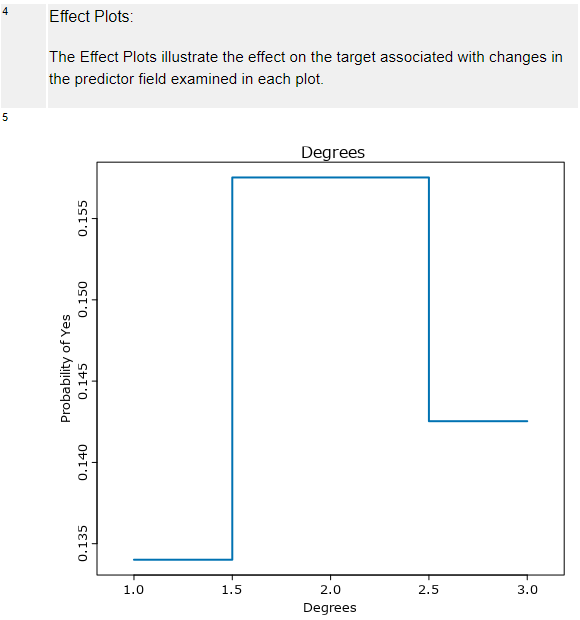
分類モデルの場合は、ターゲットごとに個別のプロットが生成されます。
この例であれば、「Degrees」が1.5以上、2.5以下であればYesになる確率が高い、ということになります。
参考
ツールマスタリーのニューラルネットワークです。

コメント