Alteryxで機械学習モデルの性能評価を行う

Alteryx Predictive Master資格取得を目指すシリーズです。

Alteryxで機械学習を使って予測した時の性能評価について確認していきたいと思います。

本記事は、Alteryxに関わらず機械学習全般についてのお話となります。

機械学習モデルの性能評価を行う際、分類と回帰で異なった指標で比較する必要があるため、それぞれ見ていきましょう。

分類

分類の場合の指標はいくつかあります。

• 混同行列（Confusion Matrix）
• 正解率、精度（Accuracy）
• 適合率（Precision）
• 再現率（Recall）もしくは感度（Sensitivity）
• 特異度（Specificity）
• F値（F-measure、F1 score）
• ROC曲線（ROC curve）
• AUC（Area Under the ROC Curve、AUROC、ROC-AUC）
• ジニ係数（Gini coefficient）
• PR曲線（Precision and recall curve）

すべてのもとになるのは混同行列です。混同行列からその他の指標を計算することが可能です。

混同行列（Confusion Matrix）

混同行列は、実際の値と予測値をマトリックス上にプロットしたものです。つまり以下のような定義の表となります（これは２値分類の場合のイメージです）。

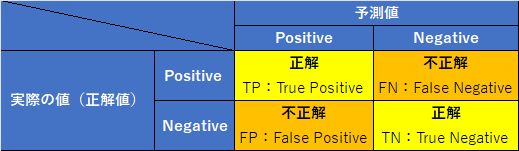
例えば、予測値がPositiveで実際の値もPositiveであれば左上の四角にプロットされます。

また、実際の値のPositiveな数は、TP＋FNとなります。NegativeなものはFP＋TNになります。

予測値のPositiveなものは、TP＋FP、Negativeなものは、FN＋TNとなります。

例えば、実際のデータは以下のようなイメージです。

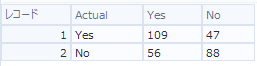
混同行列はあくまで視覚化しただけで、このままだと評価しにくいため、正解率、適合率、再現率、特異度、F値などをここから計算して比較していきます。

正解率、精度（Accuracy）

正解したレコード数÷全体のレコード数で計算したもので、正解がどれくらいあったか、を測ることができます。0～1の値の範囲を取り、1に近いほど良いということになります。

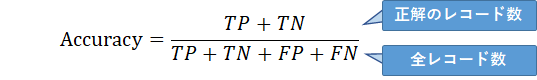
適合率（Precision）

Positiveと予測したデータのうち正解しているレコード数÷Positiveと予測したレコード数で計算したもので、Positiveと予測したうちどれくらい正解したか、を測ることができます。0～1の値の範囲を取り、1に近いほど良いということになります。

Positiveの予測の精度を測るものですが、Negativeの予測に対してどうであったかはわかりません。ただ、Negativeの予測の精度を問わない際（Negative側を正しく予測できなくても問題ないような場合）は良い指標となります。

これを言い換えると「陽性適中率」とのことです。

再現率（Recall）もしくは感度（Sensitivity）

Positiveと予測したデータのうち正解しているレコード数÷実際の値がPositiveであるレコード数で計算したもので、Positiveを正確にPositiveと予測できたかどうか、を測ることができます。0～1の値の範囲を取り、1に近いほど良いということになります。

病気かどうか、健診などで実際は病気の人を正確に病気と判断できているか、というような場合に高い値になることを期待したい指標です。ただ、誤診（誤って病気ではない人を病気で予測している可能性）については言及しない、という指標になります。つまり、Positiveの取りこぼしをしたくないような場合に有用な指標です。

なお、再現率（Recall）と適合率（Presision）にはトレードオフの関係があります。

そもそも、PositiveかNegativeか、というのは機械学習の結果では0か1かではなく、確率（％）で出力されます。つまり、Positiveが0.3でNegativeが0.7というふうに結果が出てきます。この場合、Positiveにするしきい値を0.5とすると、この結果はNegativeと判定されますが、恣意的にしきい値を変え、0.3以上をPositiveと判定するようにすると、この結果はPositiveと判定されます。これにより、再現率（Recall）が高まりますが（Positiveで予測されるものが増えるため）、適合率（Presision）は下がります（Positiveで予測されるレコードが増え、分母が増えるため）。

特異度（Specificity）

Negativeと予測したデータのうち正解しているレコード数÷実際の値がNegativeであるレコード数で計算したもので、Negativeを正確にNegativeと予測できたかどうか、を測ることができます。0～1の値の範囲を取り、1に近いほど良いということになります。つまり、再現率のNegative版です。

再現率（Recall）と特異度（Specificity）もトレードオフの関係があります。Positiveのしきい値を変えると同様にNegativeのしきい値も自動的に変わります。Positiveのしきい値を小さくする（0.5→0.3）とNegative側のしきい値は大きくなる（0.5→0.7）ため、Negative判定されるものは少なくなり、特異度は下がります。

F値（F-measure）、F1スコア（F1-score）

F値は、適合率（Precision）と再現率（Recall）のトレードオフ関係に着目し、２つの値を調和平均した値のことです。

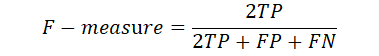
つまり、適合率（Precision）と再現率（Recall）のバランスを考えた指標となります。

ROC曲線（ROC curve）

ROCカーブは以下のようなグラフです。つまり、縦軸はTPの割合（真陽性率）、横軸がFPの割合（偽陽性率）です。

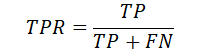
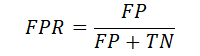
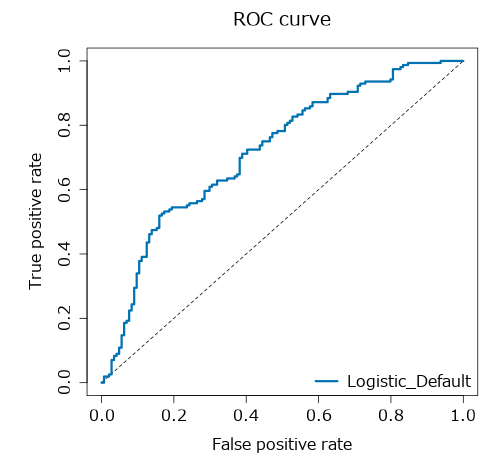
この曲線は、予測値のPositive/Negativeのしきい値を細かく0から1まで変えながらTPとFPの割合を計算し、プロットしたものです。ただし、しきい値を記載されていません。このグラフが左上に寄るほどモデルがより正しく予測できているということになります。

Alteryxでは、モデル比較ツールで取得することが可能です。

AUC（Area Under the ROC Curve、AUROC、ROC-AUC）

ROC曲線（ROC curve）の右下側の面積がAUCです。大きい方が良い、ということになります。

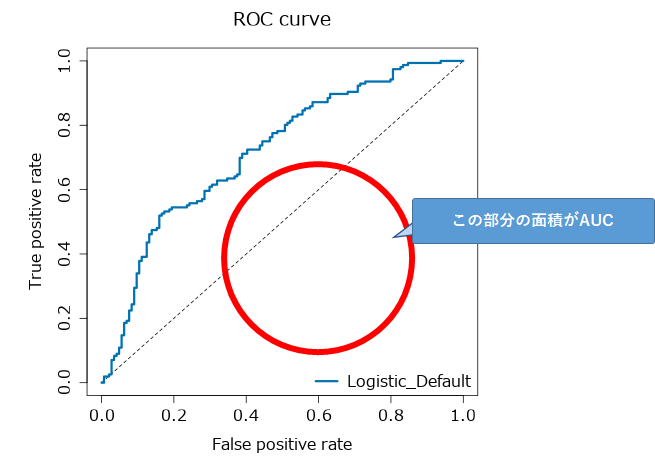
ちなみに、図の点線は、ランダムな値のときの値なので、これより高い値でないと構築したモデルに意味がないということになります。目安としては、0.9以上が高精度、0.7～0.9が適度、0.7～0.5は低精度となります。

ジニ係数（Gini coefficient）

ジニ係数（Gini coefficient）は、AUCから計算することができ、以下の式で表されます。

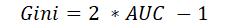
ちなみに、「社会における所得分配の不平等さを測る指標」とは異なるものなのでご注意ください。

PR曲線（Precision and recall curve）

PR曲線は、ROC曲線に似たものですが、横軸にRecall、縦軸にPrecisionをプロットしたグラフです。作り方はROC曲線と同様です。

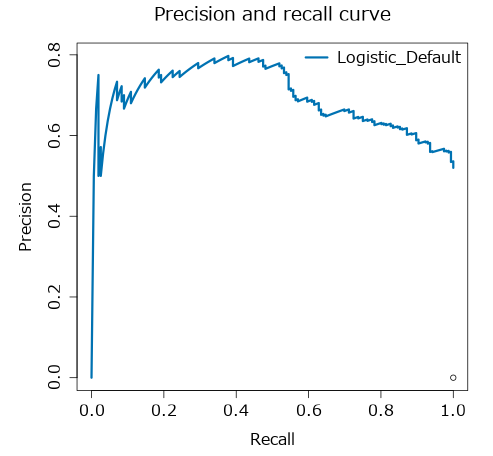
PR曲線は、ROC曲線と異なり、右肩下がりのグラフです。このグラフは、Positive/Negativeのデータが不均衡である場合に役に立つ、とされています（ROCでは、正解値がPositiveなデータ数が少なすぎるような場合、TPRがFPRよりも敏感になるため）。

回帰

回帰モデルの場合は、以下のようになります。

• RMSE（２乗平均平方根誤差）
• MSE（平均２乗誤差）
• MAE（平均絶対誤差）
• MPE（平均パーセンテージ誤差）
• MAPE（平均絶対パーセンテージ誤差）
• 決定係数（R2）
• 相関（Correlation）

MSE（平均２乗誤差）

MSEは、Mean Squared Errorで、各データに対して予測値と実際の値の差（誤差）を取り、２乗した後にそれらを合計し、データ数で割ったものです。

誤差なので、0に近いほどよいですが、２乗しているため誤差が大きいレコードを過大に評価しています。

RMSE（２乗平均平方根誤差）

RMSEは、Root Mean Squared Errorで、MSEのルート取ったものです。計算方法としては、各データに対して予測値と実際の値の差（誤差）を取り、２乗した後にそれらを合計し、データ数で割ったものをさらに平方根を取ったものです。

誤差なので、0に近いほどよいですが、２乗しているため誤差が大きいレコードを過大に評価しています。

MSEに比べると、計算時に一度２乗しているのを平方根でもとに戻しているので、単位としては元のデータに近づいているため評価はしやすくなります。

MAE（平均絶対誤差）

MAEは、Mean Absolute Errorで、各データに対して予測値と実際の値の差（誤差）を絶対値で取り、それらを合計した後に、データ数で割ったものです。

RMSEやMSEに比べると外れ値の影響を受けにくい指標となっていますが、逆に誤差が大きいレコードがあっても、評価に影響を及ぼしにくくなっています。

単位としては２乗していないため、評価しやすい指標です。

MPE（平均パーセンテージ誤差）

MPEは、Mean Percentage Errorで、各データに対して実際の値の差と予測値の差（誤差）を実際の値で割ったものを合計し、データ数で割ったものです。

絶対値や２乗していないため、プラスとマイナスで打ち消し合うので指標としては使いにくいかと思います。

MAPE（平均絶対パーセンテージ誤差）

MPEは、Mean Absolute Percentage Errorで、各データに対して実際の値の差と予測値の差（誤差）の絶対値を取ったものを実際の値で割ったものを合計し、データ数で割ったものです。

パーセンテージなのでスケールが異なるモデル間の比較などにも使えますが、一般的には使いやすくはない指標とのことです。

決定係数（R2）

決定係数（Coefficient of Determination）は、実は定義はひとつに決まっていません。また、寄与率とも呼ばれます。基本的には、1引く残差（Residual）の二乗和を全平方和で割ったもの、です。

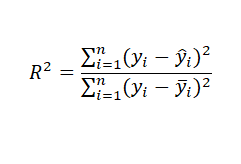
この時、各値は以下のとおりです。

なお、予測変数が増えると決定係数は１に近づくため、重回帰分析など複数の予測変数がある場合は、「自由度調整済み決定係数（Adjusted Coefficient of Determination）」が使われることが一般的です。

基本的に１に近いほど良いモデルとされます。

相関（Correlation）

Alteryxのモデル比較ツールでは、相関（Correlation）が出力されます。これは、予測値と実際の値の間の相関値です。基本的には絶対値が１に近いほど相関がある、ということになります。

例えば、以下のようなグラフが出力されます。

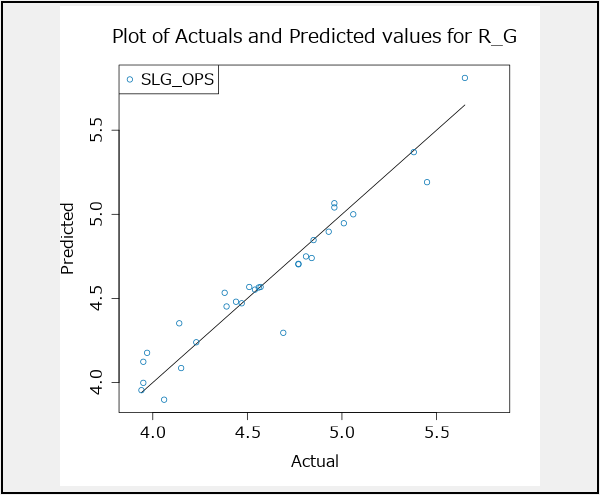
相関値としては、0.95という非常に大きな相関値となっています。

終わりに

ほぼ用語集的な形になりましたが、実際にAlteryxでモデル比較を行った結果などは「Alteryxで機械学習モデルを比較する方法」を御覧ください。

参考

• AI・機械学習の用語辞典
  • ［評価指標］正解率（Accuracy）とは？
  • ［評価指標］適合率（Precision、精度）とは？
  • ［評価指標］再現率（Recall）／感度（Sensitivity）とは？
  • ［評価指標］特異度（Specificity）とは？
  • ［評価指標］F値（F-measure、F-score）／F1スコア（F1-score）とは？
  • ［評価指標］AUC（Area Under the ROC Curve：ROC曲線の下の面積）とは？
  • ［損失関数／評価関数］平均二乗誤差（MSE：Mean Squared Error）／RMSE（MSEの平方根）とは？
  • ［損失関数／評価関数］平均絶対誤差（MAE：Mean Absolute Error）／L1損失（L1 Loss）とは？
  • ［評価関数］平均絶対パーセント誤差（MAPE：Mean Absolute Percentage Error）とは？
  • ［評価関数］決定係数（Coefficient of Determination）R2とは？

• 機械学習のモデル評価、説明可能性のための指標　その１。ジニ係数とAUC。