輸送最適化問題とは、工場からお店までの輸送コストを最適化する問題です。複数の工場があり、複数のお店が必要とする物品を輸送する際のコストを最低限にしたい、といった場合にどの配送経路を取るのが良いか、ということがわかります。
例えば、図示すると以下のようになります。
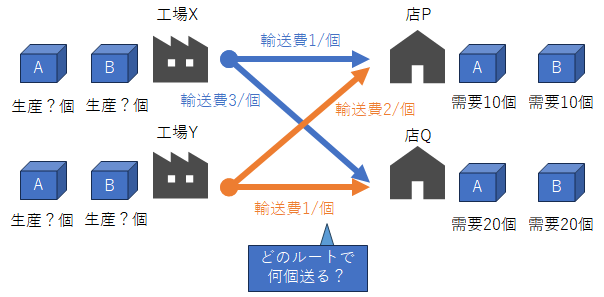
それぞれの工場の生産個数は、需要に応じて決まります。なるべく輸送費が安くなるように、どちらの工場で生産すればよいか、ということであれば、XはP、YはQで作れば輸送費が最も安いルート(おそらく工場とお店が近いのでしょう)になりますが、ここで制約条件として、工場Yの製品Aは10個までしか生産できないとします。
上の図の輸送費を表にすると、以下のようになります。
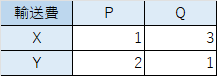
また、需要を表にしてみましょう。
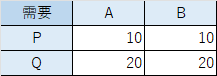
このとき、工場X、Yで生産する個数を求めたいですが、輸送費と制約条件で決まってきます。輸送個数を計算して一番小さくするようにすれば良いので、輸送する数さえ分かれば、どちらの工場で何を何個作れば良いかわかります。つまり、以下のような表を作成できます。
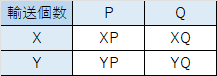
ここで、表の中の「XP」などの記号は、いわゆる変数です。XからPに送る個数は、「XP」個となります。ただ、我々がほしいのは、A、Bそれぞれどちらの工場で何個作るか、ということなので、少し式を変換してみたいと思います。
XPはX工場で作られる、AとBの製品の個数の合計×コストPです、つまり、
XP=(XA+XB)Pということになります。少し書き換えて、XP=XAP+XBPとなります。残りも同様にすると、
XQ:XAQ+XBQ
YP:YAP+YBP
YQ:YAQ+YBQ
となります。
Alteryxで輸送最適化問題を解いてみる
これらの情報を、最適化ツールのO入力、A入力、B入力にテーブルとして入力すれば最適解を解くことができます。
目的(Objective):O入力
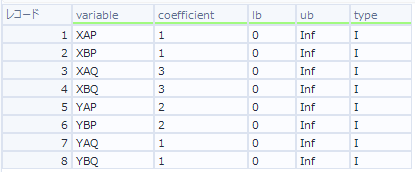
まず、O入力です。これは、欲しいものとして、各工場からお店までどの製品が何個送られるか、というのがわかればすべて得られるので、XAP、XBP、XAQ、XBQ、YAP、YBP、YAQ、YBQの8つの変数となります。配送費用を最小化したいので、coefficientは配送費用とし、最低数(lb)は0、最大数(ub)は無限(Inf)、個数なので整数(I)で求めます。これを表にすると、以下のようになります。
制約式の左辺(LHS):A入力
制約式は、需要(生産する最低数)と工場の生産可能数が当てはまります。
需要は以下の表のとおりです。

つまりPで必要となるAは10個、Bは10個で、Qで必要となるAは20個、Bは20個です。これを計算式にすると、
AP=10、BP=10、AQ=20、BQ=20
です。これを、XAP、XBP、XAQ、XBQ、YAP、YBP、YAQ、YBQで表現すると、
AP=10:XAP+YAP=10
BP=10:XBP+YBP=10
AQ=20:XAQ+YAQ=20
BQ=20:XBQ+YBQ=20
となります。
次に、生産可能数ですが、工場Yの製品Aのみ制約があります。
YA<=10
これをさらにXAP、XBP、XAQ、XBQ、YAP、YBP、YAQ、YBQで表現すると、
YAP+YAQ<=10
ということになります。
つまり、制約式の左辺は以下のような表になります。
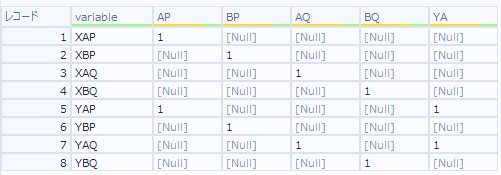
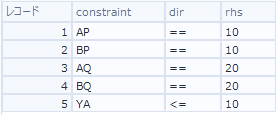
制約式の右辺(RHS):B入力
制約式の右辺は、左辺のvariableの右側のフィールドそれぞれに対応して条件を記載していきます。
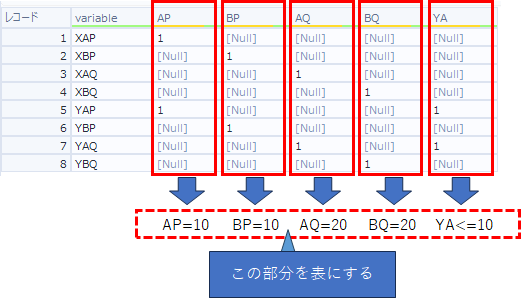
つまり、結果としては以下のようになります。
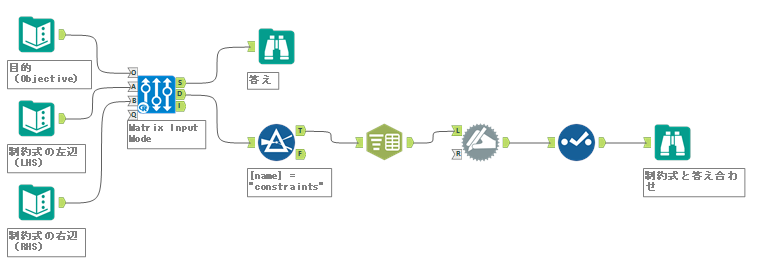
ワークフロー
ワークフローは非常に単純になります。
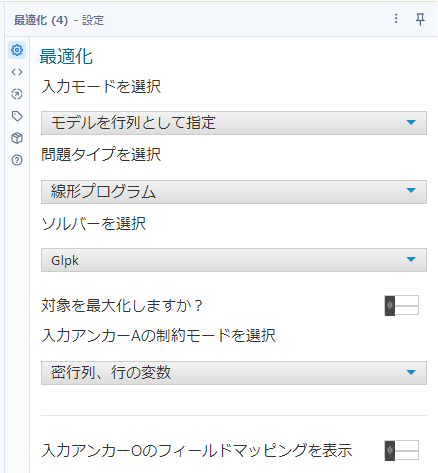
LHSの縦方向に変数(Variable)があるため、入力アンカーAの制約モードを選択オプションは、「密行列、行の変数」を選択します。
答えは以下の通り。
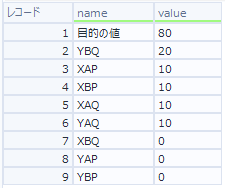
目的の値は、ここでは輸送費用になります(各輸送費Coefficient×各製品の個数を合計したもの)。これが最小化されるように、最適化ツールを設定しています。
そして、それぞれどちらの工場で何個作ってどの配送ルートに乗るか、という数が出力されています。


コメント