※過去記事はこちら。AlteryxユーザーのためのAdvent of Codeの始め方、1日目、2日目、3日目、4日目、5日目、6日目、7日目、8日目、9日目、10日目、11日目、12日目、13日目、14日目、15日目、16日目、17日目、18日目、19日目、20日目、21日目、22日目、23日目、24日目、25日目。
Advent of Code 2023の25日目は可視化することで簡単に目で判別できる問題でした(Alteryxの場合はネットワーク解析ツールを使います)。

しかしながら、ちゃんとロジックでもって解きたいですよね(AlteryxのBaseAルールとして結構グレーな感じもするので)。
しかしながら、1408ノード、3148エッジのグラフを総当りで解くには3148x3148x3148=31,196,377,792パターン調べる必要があります。これはなかなかしんどそうなので、何かしらアルゴリズムが必要そうです。今回はこの問題を最小カット問題と捉えて、永持-茨木法で解いてみましょう。
AoC 2023 Day25の問題
あるグラフがあり、最小カットは3というのがわかっていますが、その3本を特定することです。上の図からは目視で3本がすぐにわかります。
永持-茨木法とは?
京都大学の方が考案されたアルゴリズムのようで、こちらに解説があります。というか、ほぼここにしか解説がなくてちょっと情報が少なすぎでした・・・(ホームページによると、最小カット問題を解くための最速のアルゴリズムとのことです)。
このアルゴリズムは、最大隣接順序と呼ばれるものをグラフのノードに対してふっていきます。つまり各ノードに番号をつけていくわけですが、最初に番号をふったノードに対して最も結びつきの強い(結びついているエッジの数が多い)ノードを選択していきます。その後、一番最後に番号をつけたノードをグラフからカットし、その際のカット数を控えます。さらに最後に番号をつけたノードと一つ前に番号をつけたノードを合体します(ノードリストとエッジリストを更新する必要があります)。これを繰り返し、控えたカット数で一番小さいものが最小カット数です。
今回の問題を解くためには、どのエッジをカットする必要があるのか、を調べる必要があるので、それぞれの最大隣接順序の最後のノードを記録しておく必要があります。
最大隣接順序の作り方
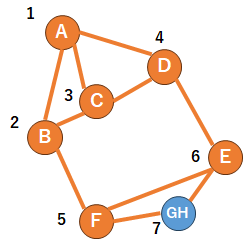
最初のノードはランダムに選べばオッケーですが、選択したノードと結びつきの強いノードを次々と選んでいきます。まず、以下のようなグラフを考えてみましょう。
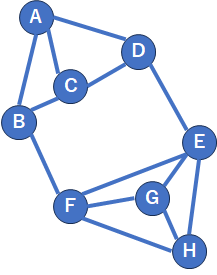
1.最初にまずランダムにAを選択してみます。
2.次に、Aと結びつきの強いノードはB、C、Dのいずれかです。どれでもいいので1本選びます。例えばBにしましょう)。
3.今、AとBが選択されていますが、この選択済みのグループに対して結びつきの強いものは、、、候補としてC、D、Fですね(エッジが接続されているため)。
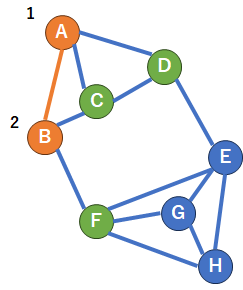
4.それぞれの結びつきの強さは、Cが2本、DとFは1本のエッジでA、Bのグループと接続されています。つまり、今回はCを選択します。
5.これを繰り返していくと、以下のようになります。これが最大隣接順序です。
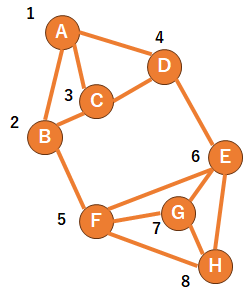
最大隣接順序の性質
最大隣接順序には性質があり、
この番号付けにおいて,最後の二つの節点(A, Bとする)に対しては,節点 A と節点 B を別々のグループに分 けるような分割の中では,最後の節点1個とそれ以外の節点を分けるのが,最も分割の両側にまたがる枝の数値 和が小さくなることが証明されています.
https://www-or.amp.i.kyoto-u.ac.jp/demo/MINCUT.html
とのことです。この永持-茨木法というのはこの性質を使用している、ということになるでしょう。
最大隣接順序を作ったあとに行うこと
性質はおいといて、ここからまた作業があります。
6.最後に付けた2つのノードに着目します。今回だと、7と8です(GとH)。
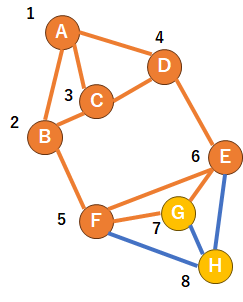
7.ここで、グラフから8をカットします。上の図を見ると、8を元のグラフから切り離すには、1~7と8をつなぐ三本のエッジを削除すればオッケーです(図の青い部分)。このカットした時のエッジの本数を控えておきましょう(これをカット数と言います)。
8.最後の2つのノードを併合します。ノードリストとエッジリストの更新が必要になるかと思います。これで1ループです。
9.1~8を繰り返すことで、ノードの数が減っていきますが、これを一つのノードになるまで繰り返します。
10.7で記録したカット数のうち、最小のものが最小カットです。
Alteryxでやってみましょう
以下は、Alteryxをそれなりに(少なくとも各アイコンの意味を理解していること)理解していないと理解できない部分かと思います。
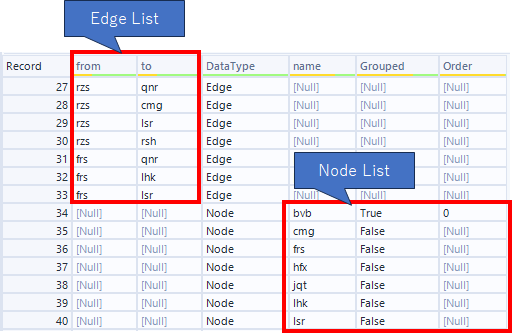
データとしては、ノードリスト、
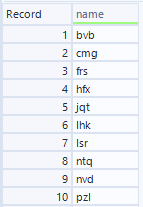
そして、エッジリストを使います。
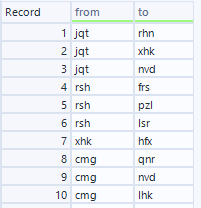
これをスタートのデータから作るためには以下のようなWFとなります。
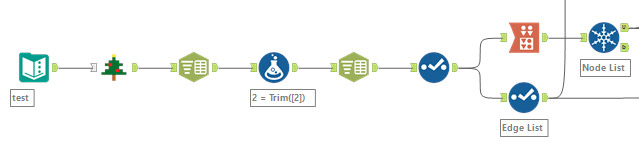
次に、Alteryxの反復マクロは繰り返すデータストリームを一つしか持てないので、これらをマクロ内で使える形にした後にノードリストとエッジリストを結合します。
ワークフローは以下の通り。
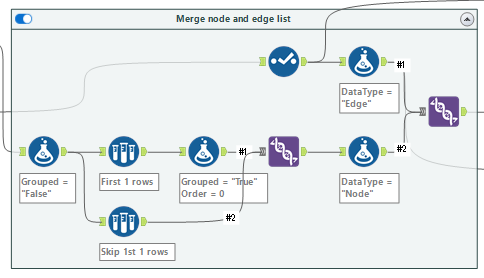
ここまでが永持-茨木法を適用するための準備です。
次に、最大隣接順序をマクロで作っていきましょう。最大隣接順序を作るための1~7の繰り返しを行うマクロと、最大隣接順序の最後の2つのノードを結合して再度最大隣接順序を作るための6~8を繰り返すための外側のマクロの2つのマクロが必要です。
外側のマクロ全景です。
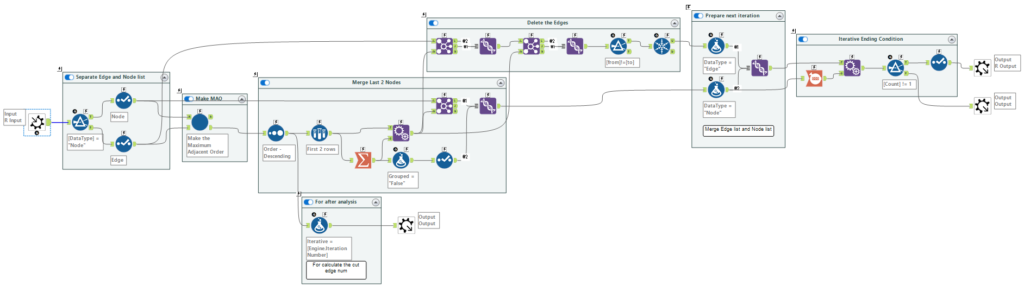
ノードリスト、エッジリストにデータを分離し、最大隣接順序を作るマクロにデータを入れ、出てきたリストに対してラスト2ノードを結合し、ノードリスト、エッジリストをアップデートし、再度繰り返すためにノードリストとエッジリストを併合する、という形になっています。
最大隣接順序を作るマクロ全景です。

このマクロ内では、ノードリストのみ書き換わるため、エッジリストは固定的な入力になっています。グループ化されたノードリストから次に接続する可能性のある候補ノードを抽出し、結びつきの強いノードを選択し、繰り返しのためのノードリストを更新している、といった感じです。
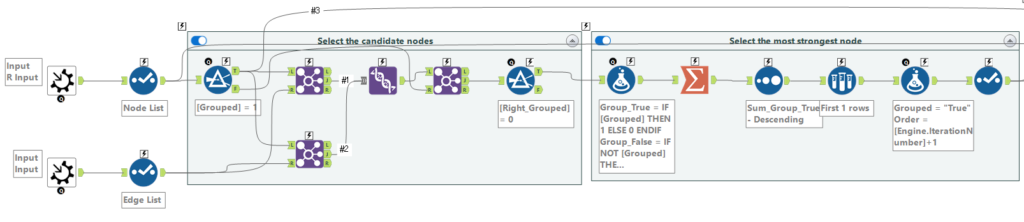
アルゴリズムのメイン部分を拡大した図が上の部分です。左側のブロックで候補ノードの抽出を行い、右側のブロックで結びつきの強いノードを決めています。
再びマクロの外に戻りましょう。このマクロにより、最大隣接順序が複数得られます。それぞれの最大隣接順序のリストにおいて、最後に選択されたノードを抽出します。
これ、データを実際に見てみましょう。例えば、テストデータの11回目の反復では以下のようなデータが得られています。

すでにノードが併合されて4レコードしかありません。一番上のrhn-jqtという合体ノードをカットした時のカットするのに必要なエッジの本数を計算すれば、カット数が出てきます。
これを行っているのが、以下の部分です。
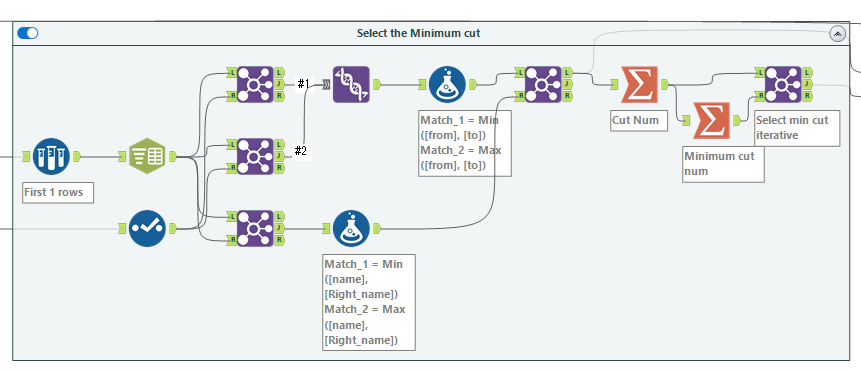
これで、どの反復時が最小カットだったのか、が出てきます。

あとは、削除するべきエッジのリストを算出し、クイズの答えを計算するだけです。
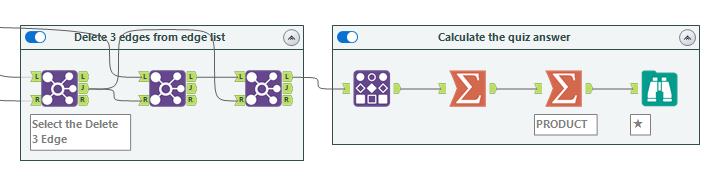
ワークフロー全景です。

まとめ
Advent of Code 2023年の25日目の問題は、可視化することで削除すべきエッジを発見して解きましたが、なんらかのロジックで解いたわけではないので、ちゃんとしたロジックで解くという宿題をようやく解決できました。
そもそも永持-茨木法を実装するのが手探りだったので、ほんとにこれでうまくいくの?という感じで実装をしたのでAoC2023の25問目に必ずしも最適化されていません。ただし、永持-茨木法としての機能はうまく実装できていると思います。
Alteryxの場合、反復マクロが遅いので、2重ループだと余計に時間がかかるようです。外側のループはノード数の1408回回りますが、内部ループはノードが徐々に少なくなるので1レコードずつ反復回数が減っていきます(しかも、レコード数自体もノードが併合されていくので減っていきます)。なので、徐々に反復速度が早くなると思われます。
私のAoCのクイズの問題では、781反復で最小カット3が出ていたので、この時点で止めるように作ればもっと早く結果が出ましたね・・・まぁ、今回は永持-茨木法をAlteryxで実装するのを主題にしていたので、カット数を出す部分をマクロの外に出してしまっていました。そういう意味ではAoC2023D25に特化するならもう少し最適化が可能です。ちなみに、テストデータでは1.2秒で結果が出ますが、フルデータでは3時間24分かかっていました・・・。



コメント