※過去記事はこちら。AlteryxユーザーのためのAdvent of Codeの始め方、1日目、2日目、3日目、4日目、5日目、6日目、7日目、8日目、9日目、10日目、11日目、12日目、13日目、14日目、15日目、16日目、17日目、18日目、19日目、20日目、21日目
22日目です。22のPart2が解けたときの画像を採用しています。

タイトルは、「Monkey Map」。猿の地図ですね・・・。
今回の問題は、立方体のキューブの周りを指示に沿って進む問題です。ストーリー的には力場で守られているところに侵入するのにパスワードが必要とのこと。パスワードはこの地図を通るとわかる、とのことです。
サンプルの入力データとしては、以下のようになっています。
...#
.#..
#...
....
...#.......#
........#...
..#....#....
..........#.
...#....
.....#..
.#......
......#.
10R5L5R10L4R5L5上部は地図、下部の数値が入った文字列は進むルートです。
上の地図の#は壁。「.」はなにもないところです。空白の部分は虚無なので進めません。壁も超えて進めません。
下の部分は進むべきルートです。数字は進むマスの数。Lは左に向く、Rは右に向く、です。
壁にあたったら進むマスの数を進めてなくてもそこで止まる必要があります。また、地図の端に来た時は、逆側にループして出現します。ドラクエの地図の端みたいなものです。
ルート通り進み終えると、パスワードがわかります。若干この計算面倒ですが、最後のポイントの行×1000+最後のポイントの列×4+最終ポイントの向き(右:0、下:1、左:2、上:3)で計算されます。
Part2は、地図の端に到達したときの処理がかわります。図形を立体的に考えたときの接続されている辺に出てくるとのことです。それ以外のルールはPart1と同じです。
・ネ
・
・タ
・
・バ
・
・レ
解いてみる
地道に指示通りの処理を行うだけです。反復マクロで指示データを一行ごと実行していくようにしました。

処理マクロ:
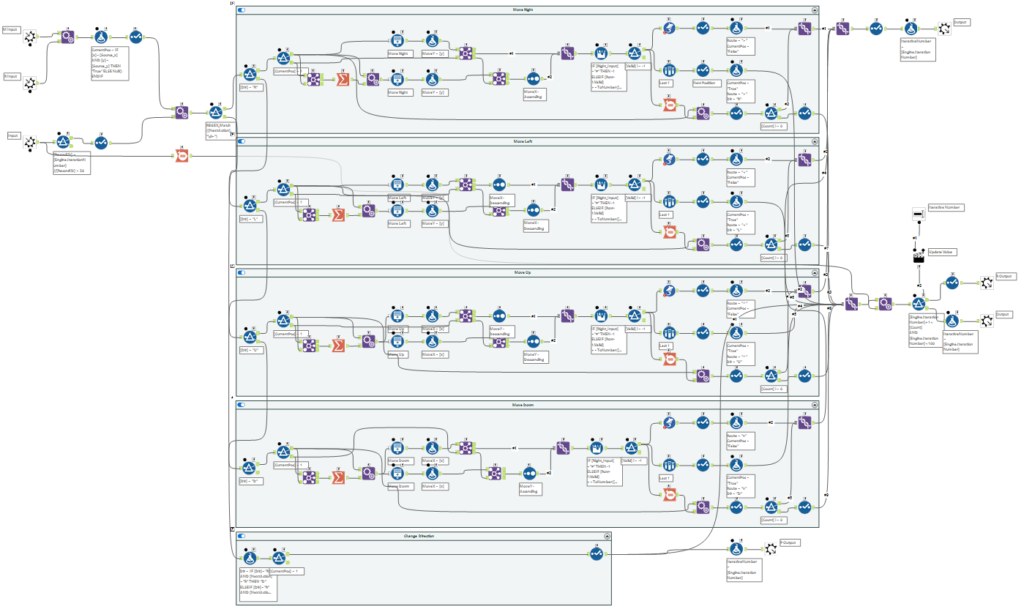
最初、反復するデータの中にすべての地図データも入れて反復していたので、30分も実行にかかるマクロになっていました。これを、現在のポイントのみ反復するように書き換えて、7分で終わるようになりました。やはり、1万5000レコードを繰り返し処理すると時間がかかります。
マクロ書き換え後の入力データは、地図データ、動きを指示するデータ(内部的にはIterativeNumber変数を使ってフィルターして抽出します)、現在のポイントデータという形で分けています。
ロジックをわかりやすくするために多くのツールで構成していますが、その分処理に時間がかかるようになってしまっています。
Part2は、未解決ですので、解けたらアップします。地図の端に来たときの処理をうまくする必要があるのでその部分だけうまくロジックを加えることができればほぼその他そのままでいけそうではあります。
Part2はデバッグに非常に時間がかかってしまいました。基本的にPart1のマクロをいじってなんとかしようとしたのですが、どうしてもバグが取れなかったので、改めて作り直しました。フィルターツールで場合分けしていたのを一本化し、シンプルなマクロにしています。もとのマクロと新しいマクロの結果を比較しながら最終的にデバッグできました。しかし、作り直しのおかげで7分かかっていたマクロが2分かからず完了するようになりました。
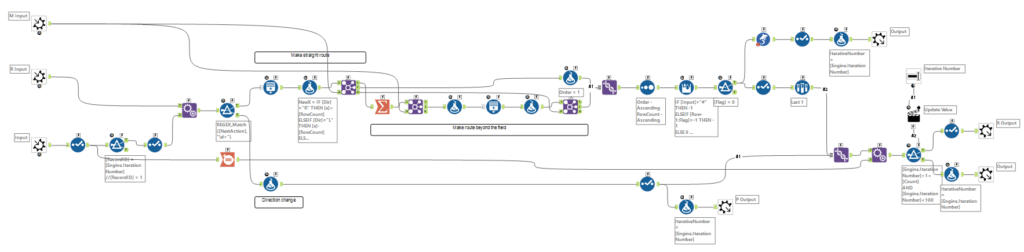
デバッグに時間がかかった一番の理由は、Part1と違って目で追えないことです。面をまたぐ際に、どう動くのが正解なのか、ぱっと見れない、というところが一番苦労したポイントです。とはいえ、見通しの悪いマクロというのも良くないですね・・・。
また、サンプルデータと本番データで立方体の展開図が異なるため、サンプルデータでの動きが確認できていないところもポイントです。
ちなみに、立方体の辺のマッピングですが、まず、関係性を書くと以下のような感じでした。
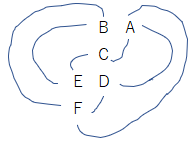
実際は軸が反転したりするので、これだとわかりにくいので、少し書き換えますと・・・
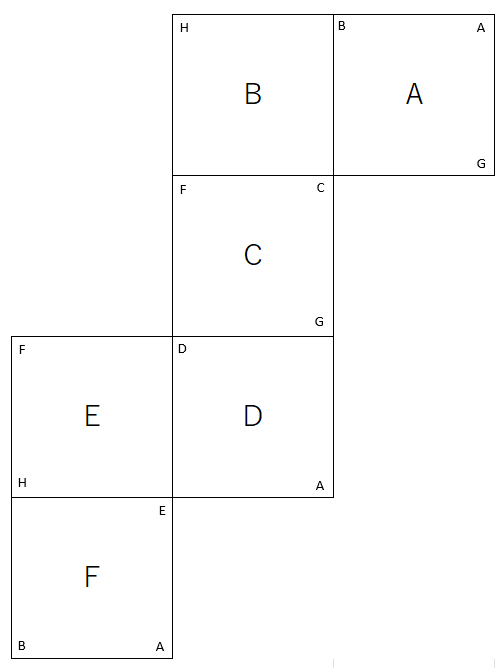
こんな感じになります。面をアルファベットでつけているのに、さらに軸をアルファベットで書いてしまったので、わかりにくいかもしれませんが、軸を書くとどこからどこに行った際に軸が反転するかがわかりやすくなります。さらに、情報を追記します。
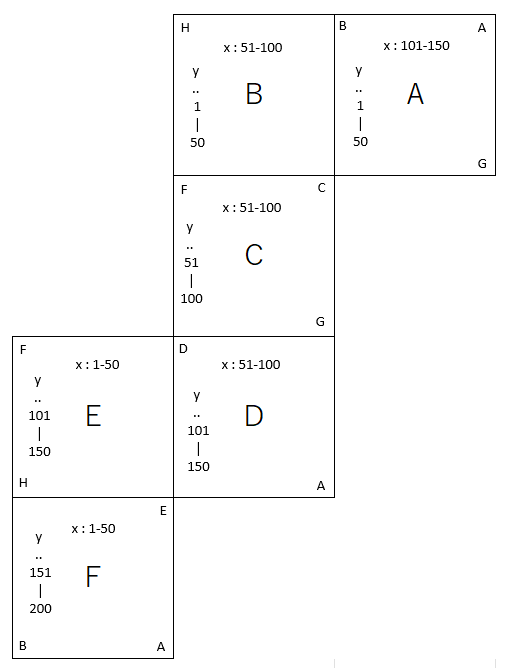
これを表にまとめると、以下のようになります。
| 動く方向 | 今の面 | 移動先 | 移動先で動く方向 | 軸の方向 | 移動先のx | 移動先のy |
|---|---|---|---|---|---|---|
| R(右) | A | D | L(左) | 反転 | 100 | 150-y+1 |
| R(右) | C | A | U(上) | y+50 | 50 | |
| R(右) | D | A | L(左) | 反転 | 150 | 150-y+1 |
| R(右) | F | D | U(上) | y-100 | 150 | |
| L(左) | B | E | R(右) | 反転 | 1 | 150-y+1 |
| L(左) | C | E | D(下) | y+50 | 101 | |
| L(左) | E | B | R(右) | 反転 | 51 | 150-y+1 |
| L(左) | F | B | D(下) | y-100 | 1 | |
| U(上) | A | F | U(上) | x-100 | 200 | |
| U(上) | B | F | R(右) | 反転 | 1 | 150-y+1 |
| U(上) | E | C | R(右) | 51 | x+50 | |
| D(下) | A | C | L(左) | 100 | x-50 | |
| D(下) | D | F | L(左) | 50 | y+100 | |
| D(下) | F | A | D(下) | x | 200 |
このような表の中身を面をまたぐ際に組み込んでいきます。
正解データがあればもっと早くできるんですが、ないとなかなか厳しいですね・・・。
最終的なワークフローは以下のとおりです。
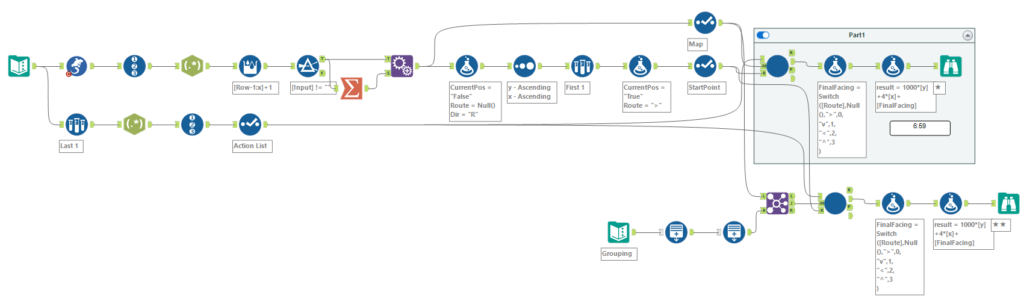
ちなみに、私の入力データと同じ展開図じゃないと正常動作しないのでご注意ください。
まとめ
- 22日目はまたもや地図の問題でした。地図の端に達したときの処理が面倒です。また、サンプルデータは本番データで起こりうる処理のすべてのパターンを網羅していないので、本番データでもしっかりデバッグする必要があるかもしれません。
- 難易度は非常に高く、Part2まで解いているのは3名しかいません。Part1までは解けてもPart2で止まる傾向のようです・・・。
- 個人タイム:数日かけてPart1まで解きました。Part2はかなりデバッグに時間がかかり、最も時間がかかったものの一つです。マクロを作り直す前は行き詰まっていてちょっとどうしようかと思いました・・・。


コメント